Mathematics

LU Factorization

LU factorization, or Gaussian elimination, expresses any square matrix A as the product of a permutation of a lower triangular matrix and an upper triangular matrix

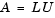
where L is a permutation of a lower triangular matrix with ones on its diagonal and U is an upper triangular matrix.

The permutations are necessary for both theoretical and computational reasons. The matrix

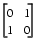
cannot be expressed as the product of triangular matrices without interchanging its two rows. Although the matrix

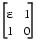
can be expressed as the product of triangular matrices, when 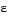is small the elements in the factors are large and magnify errors, so even though the permutations are not strictly necessary, they are desirable. Partial pivoting ensures that the elements of L are bounded by one in magnitude and that the elements of U are not much larger than those of A.

For example

• [L,U] = lu(B)
  
  L =
      1.0000         0         0
      0.3750    0.5441    1.0000
      0.5000    1.0000         0
  
  U =
      8.0000    1.0000    6.0000
           0    8.5000   -1.0000
           0         0    5.2941
  

The LU factorization of A allows the linear system

• A*x = b
  

to be solved quickly with

• x = U\(L\b)
  

Determinants and inverses are computed from the LU factorization using

• det(A) = det(L)*det(U)
  

and

• inv(A) = inv(U)*inv(L)
  

You can also compute the determinants using det(A) = prod(diag(U)), though the signs of the determinants may be reversed.

Cholesky Factorization

QR Factorization

© 1994-2005 The MathWorks, Inc.