

| Mathematics |   |
Matrix Powers and Exponentials
This section tells you how to obtain the following matrix powers and exponentials in MATLAB:
Positive Integer Powers
If A is a square matrix and p is a positive integer, then A^p effectively multiplies A by itself p-1 times. For example,
Inverse and Fractional Powers
If A is square and nonsingular, then A^(-p) effectively multiplies inv(A) by itself p-1 times.
Fractional powers, like A^(2/3), are also permitted; the results depend upon the distribution of the eigenvalues of the matrix.
Element-by-Element Powers
The .^ operator produces element-by-element powers. For example,
Exponentials
computes A^(1/2) by a more accurate algorithm. The m in sqrtm distinguishes this function from sqrt(A) which, like A.^(1/2), does its job element-by-element.
A system of linear, constant coefficient, ordinary differential equations can be written
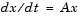
where x = x(t) is a vector of functions of t and A is a matrix independent of t. The solution can be expressed in terms of the matrix exponential,
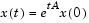
computes the matrix exponential. An example is provided by the 3-by-3 coefficient matrix
and the initial condition, x(0)
The matrix exponential is used to compute the solution, x(t), to the differential equation at 101 points on the interval 0 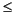 t
t 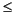 1 with
1 with
A three-dimensional phase plane plot obtained with
shows the solution spiraling in towards the origin. This behavior is related to the eigenvalues of the coefficient matrix, which are discussed in the next section.
 | QR Factorization | Eigenvalues |  |
© 1994-2005 The MathWorks, Inc.