Mathematics

Example -- Writing M-Files for Different Data Types

If you write an M-file that works with data of type single or double, the M-file might need to return different answers depending on the data type. The following example illustrates this.

Computing the Ratios of Fibonacci Numbers

The Fibonacci numbers are the numbers f_n defined recursively by

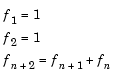
The first seven numbers in the Fibonacci sequence are 1, 1, 2, 3, 5, 8, 13. As n gets larger, the ratio of the n+1st Fibonacci number divided by the nth Fibonacci number tends to the golden mean, 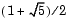. That is,

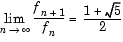
Suppose you want to compute how large n must be so that the ratio

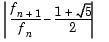
is within eps of the golden mean. The answer depends on whether you are computing in single or double-precision arithmetic, because the value of eps((1+sqrt(5))/2) depends on the data type of the golden mean.

• eps((1+sqrt(5))/2)
  
  ans =
  
    2.2204e-016
  

while

• eps(single((1+sqrt(5))/2))
  
  ans =
  
    1.1921e-007
  

You can write an M-file to compute the answer in either case, by passing in the data type as an input argument. The following code shows how to do this.

• function count = fib(data_type)
  f_current = ones(1,1,data_type);
  f_next = f_current;
  golden_mean = (1+sqrt(5))/2*ones(1,1,data_type);
  count = 0;
  while abs(f_next/f_current - golden_mean) >= eps(golden_mean)
      count = count + 1;
      temp = f_next;
      f_next = f_next + f_current;
      f_current = temp;
  end
  

The output count is the smallest integer for which

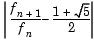
is smaller than eps(golden_mean).

For double-precision arithmetic, the answer is

• fib('double')
  
  ans =
  
      39
  

For single-precision arithmetic, the answer is

• fib('single')
  
  ans =
  
      17
  

The Function eps

Largest and Smallest Numbers of Type double and single

© 1994-2005 The MathWorks, Inc.