Factorization :: Sparse Matrices (Mathematics)

Mathematics

Factorization

This section discusses four important factorization techniques for sparse matrices:

LU, or triangular, factorization
Cholesky factorization
QR, or orthogonal, factorization
Incomplete factorizations

LU Factorization

If S is a sparse matrix, the following command returns three sparse matrices L, U, and P such that P*S = L*U.

```
[L,U,P] = lu(S)
```

lu obtains the factors by Gaussian elimination with partial pivoting. The permutation matrix P has only n nonzero elements. As with dense matrices, the statement [L,U] = lu(S) returns a permuted unit lower triangular matrix and an upper triangular matrix whose product is S. By itself, lu(S) returns L and U in a single matrix without the pivot information.

The three-output syntax

```
[L,U,P] = lu(S)
```

selects P via numerical partial pivoting, but does not pivot to improve sparsity in the LU factors. On the other hand, the four-output syntax

```
[L,U,P,Q]=lu(S) 
```

selects P via threshold partial pivoting, and selects P and Q to improve sparsity in the LU factors.

You can control pivoting in sparse matrices using

```
lu(S,thresh)
```

where thresh is a pivot threshold in [0,1]. Pivoting occurs when the diagonal entry in a column has magnitude less than thresh times the magnitude of any sub-diagonal entry in that column. thresh = 0 forces diagonal pivoting. thresh = 1 is the default.

MATLAB automatically allocates the memory necessary to hold the sparse L and U factors during the factorization. MATLAB does not use any symbolic LU prefactorization to determine the memory requirements and set up the data structures in advance.

Reordering and Factorization. If you obtain a good column permutation p that reduces fill-in, perhaps from symrcm or colamd, then computing lu(S(:,p)) takes less time and storage than computing lu(S). Two permutations are the symmetric reverse Cuthill-McKee ordering and the symmetric minimum degree ordering.

```
r = symrcm(B);
m = symamd(B);
```

The three spy plots produced by the lines below show the three adjacency matrices of the Bucky Ball graph with these three different numberings. The local, pentagon-based structure of the original numbering is not evident in the other three.

```
spy(B)
spy(B(r,r))
spy(B(m,m))
```

The reverse Cuthill-McKee ordering, r, reduces the bandwidth and concentrates all the nonzero elements near the diagonal. The approximate minimum degree ordering, m, produces a fractal-like structure with large blocks of zeros.

To see the fill-in generated in the LU factorization of the Bucky ball, use speye(n,n), the sparse identity matrix, to insert -3s on the diagonal of B.

```
B = B - 3*speye(n,n);
```

Since each row sum is now zero, this new B is actually singular, but it is still instructive to compute its LU factorization. When called with only one output argument, lu returns the two triangular factors, L and U, in a single sparse matrix. The number of nonzeros in that matrix is a measure of the time and storage required to solve linear systems involving B. Here are the nonzero counts for the three permutations being considered.

Original
lu(B)
1022

Reverse Cuthill-McKee
lu(B(r,r))
968

Approximate minimum degree
lu(B(m,m))
636

Original	`lu(B)`	1022
Reverse Cuthill-McKee	`lu(B(r,r))`	968
Approximate minimum degree	`lu(B(m,m))`	636

Even though this is a small example, the results are typical. The original numbering scheme leads to the most fill-in. The fill-in for the reverse Cuthill-McKee ordering is concentrated within the band, but it is almost as extensive as the first two orderings. For the minimum degree ordering, the relatively large blocks of zeros are preserved during the elimination and the amount of fill-in is significantly less than that generated by the other orderings. The spy plots below reflect the characteristics of each reordering.

three spy plots showing the characteristics of each reordering

Cholesky Factorization

If S is a symmetric (or Hermitian), positive definite, sparse matrix, the statement below returns a sparse, upper triangular matrix R so that R'*R = S.

```
R = chol(S)
```

chol does not automatically pivot for sparsity, but you can compute minimum degree and profile limiting permutations for use with chol(S(p,p)).

Since the Cholesky algorithm does not use pivoting for sparsity and does not require pivoting for numerical stability, chol does a quick calculation of the amount of memory required and allocates all the memory at the start of the factorization. You can use symbfact, which uses the same algorithm as chol, to calculate how much memory is allocated.

QR Factorization

MATLAB computes the complete QR factorization of a sparse matrix S with

```
 [Q,R] = qr(S)
```

but this is usually impractical. The orthogonal matrix Q often fails to have a high proportion of zero elements. A more practical alternative, sometimes known as "the Q-less QR factorization," is available.

With one sparse input argument and one output argument

```
R = qr(S)
```

returns just the upper triangular portion of the QR factorization. The matrix R provides a Cholesky factorization for the matrix associated with the normal equations,

```
R'*R = S'*S
```

However, the loss of numerical information inherent in the computation of S'*S is avoided.

With two input arguments having the same number of rows, and two output arguments, the statement

```
[C,R] = qr(S,B)
```

applies the orthogonal transformations to B, producing C = Q'*B without computing Q.

The Q-less QR factorization allows the solution of sparse least squares problems

with two steps

```
[c,R] = qr(A,b)
x = R\c
```

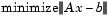
If A is sparse, but not square, MATLAB uses these steps for the linear equation solving backslash operator

```
x = A\b
```

Or, you can do the factorization yourself and examine R for rank deficiency.

It is also possible to solve a sequence of least squares linear systems with different right-hand sides, b, that are not necessarily known when R = qr(A) is computed. The approach solves the "semi-normal equations"

```
R'*R*x = A'*b
```

with

```
x = R\(R'\(A'*b))
```

and then employs one step of iterative refinement to reduce roundoff error

r = b - A*x
e = R\(R'\(A'*r))
x = x + e

Incomplete Factorizations

The luinc and cholinc functions provide approximate, incomplete factorizations, which are useful as preconditioners for sparse iterative methods.

The luinc function produces two different kinds of incomplete LU factorizations, one involving a drop tolerance and one involving fill-in level. If A is a sparse matrix, and tol is a small tolerance, then

```
[L,U] = luinc(A,tol)
```

computes an approximate LU factorization where all elements less than tol times the norm of the relevant column are set to zero. Alternatively,

```
[L,U] = luinc(A,'0')
```

computes an approximate LU factorization where the sparsity pattern of L+U is a permutation of the sparsity pattern of A.

For example,

load west0479
A = west0479;
nnz(A)
nnz(lu(A))
nnz(luinc(A,1e-6))
nnz(luinc(A,'0'))

shows that A has 1887 nonzeros, its complete LU factorization has 16777 nonzeros, its incomplete LU factorization with a drop tolerance of 1e-6 has 10311 nonzeros, and its lu('0') factorization has 1886 nonzeros.

The luinc function has a few other options. See the luinc reference page for details.

The cholinc function provides drop tolerance and level 0 fill-in Cholesky factorizations of symmetric, positive definite sparse matrices. See the cholinc reference page for more information.

Permutation and Reordering Simultaneous Linear Equations