Mathematics

Simultaneous Linear Equations

There are two different classes of methods for solving systems of simultaneous linear equations:

• Direct methods are usually variants of Gaussian elimination. These methods involve the individual matrix elements directly, through matrix factorizations such as LU or Cholesky factorization. MATLAB implements direct methods through the matrix division operators / and \, which you can use to solve linear systems.
• Iterative methods produce only an approximate solution after a finite number of steps. These methods involve the coefficient matrix only indirectly, through a matrix-vector product or an abstract linear operator. Iterative methods are usually applied only to sparse matrices.

Direct Methods

Direct methods are usually faster and more generally applicable than indirect methods, if there is enough storage available to carry them out. Iterative methods are usually applicable to restricted cases of equations and depend upon properties like diagonal dominance or the existence of an underlying differential operator. Direct methods are implemented in the core of MATLAB and are made as efficient as possible for general classes of matrices. Iterative methods are usually implemented in MATLAB M-files and may make use of the direct solution of subproblems or preconditioners.

Using a Different Preordering.   If A is not diagonal, banded, triangular, or a permutation of a triangular matrix, backslash (\) reorders the indices of A to reduce the amount of fill-in -- that is, the number of nonzero entries that are added to the sparse factorization matrices. The new ordering, called a preordering, is performed before the factorization of A. In some cases, you might be able to provide a better preordering than the one used by the backslash algorithm.

To use a different preordering, first turn off the automatic preordering that backslash performs by default, using the function spparms as follows:

• spparms('autoamd',0);
  spparms('autommd',0);
  

Now, assuming you have created a permutation vector p that specifies a preordering of the indices of A, apply backslash to the matrix A(:,p), whose columns are the columns of A, permuted according to the vector p.

• x = A (:,p) \ b;
  x(p) = x;
  spparms('autoamd',1);
  spparms('autommd',1);
  

The commands spparms('autoamd',1) and spparms('autommd',1) turns the automatic preordering back on, in case you use A\b later without specifying an appropriate preordering.

Iterative Methods

Nine functions are available that implement iterative methods for sparse systems of simultaneous linear systems.

Functions for Iterative Methods for Sparse Systems  

Function	Method
bicg	Biconjugate gradient
bicgstab	Biconjugate gradient stabilized
cgs	Conjugate gradient squared
gmres	Generalized minimum residual
lsqr	LSQR implementation of Conjugate Gradients on the Normal Equations
minres	Minimum residual
pcg	Preconditioned conjugate gradient
qmr	Quasiminimal residual
symmlq	Symmetric LQ

These methods are designed to solve 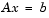or 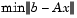. For the Preconditioned Conjugate Gradient method, pcg, A must be a symmetric, positive definite matrix. minres and symmlq can be used on symmetric indefinite matrices. For lsqr, the matrix need not be square. The other five can handle nonsymmetric, square matrices.

All nine methods can make use of preconditioners. The linear system

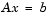
is replaced by the equivalent system

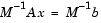
The preconditioner M is chosen to accelerate convergence of the iterative method. In many cases, the preconditioners occur naturally in the mathematical model. A partial differential equation with variable coefficients may be approximated by one with constant coefficients, for example. Incomplete matrix factorizations may be used in the absence of natural preconditioners.

The five-point finite difference approximation to Laplace's equation on a square, two-dimensional domain provides an example. The following statements use the preconditioned conjugate gradient method preconditioner M = R'*R, where R is the incomplete Cholesky factor of A.

• A = delsq(numgrid('S',50));
  b = ones(size(A,1),1);
  tol = 1.e-3;
  maxit = 10;
  R = cholinc(A,tol);
  [x,flag,err,iter,res] = pcg(A,b,tol,maxit,R',R);
  

Only four iterations are required to achieve the prescribed accuracy.

Background information on these iterative methods and incomplete factorizations is available in [2] and [7].

Factorization

Eigenvalues and Singular Values

© 1994-2005 The MathWorks, Inc.