

| MATLAB Function Reference |   |
Syntax
Description
MATLAB has two different types of arithmetic operations. Matrix arithmetic operations are defined by the rules of linear algebra. Array arithmetic operations are carried out element by element, and can be used with multidimensional arrays. The period character (.) distinguishes the array operations from the matrix operations. However, since the matrix and array operations are the same for addition and subtraction, the character pairs .+ and .- are not used.
Addition or unary plus. A+B adds A and B. A and B must have the same size, unless one is a scalar. A scalar can be added to a matrix of any size. |
|
Subtraction or unary minus. A-B subtracts B from A. A and B must have the same size, unless one is a scalar. A scalar can be subtracted from a matrix of any size. |
|
Matrix multiplication. C = A*B is the linear algebraic product of the matrices A and B. More precisely,For nonscalar A and B, the number of columns of A must equal the number of rows of B. A scalar can multiply a matrix of any size. |
|
Array multiplication. A.*B is the element-by-element product of the arrays A and B. A and B must have the same size, unless one of them is a scalar. |
|
Slash or matrix right division. B/A is roughly the same as B*inv(A). More precisely, B/A = (A'\B')'. See the reference page for mrdivide for more information. |
|
Array right division. A./B is the matrix with elements A(i,j)/B(i,j). A and B must have the same size, unless one of them is a scalar. |
|
Backslash or matrix left division. If A is a square matrix, A\B is roughly the same as inv(A)*B, except it is computed in a different way. If A is an n-by-n matrix and B is a column vector with n components, or a matrix with several such columns, then X = A\B is the solution to the equation AX = B computed by Gaussian elimination. A warning message is displayed if A is badly scaled or nearly singular. See the reference page for mldivide for more information. |
|
If A is an m-by-n matrix with m ~= n and B is a column vector with m components, or a matrix with several such columns, then X = A\B is the solution in the least squares sense to the under- or overdetermined system of equations AX = B. The effective rank, k, of A is determined from the QR decomposition with pivoting (see Algorithm for details). A solution X is computed that has at most k nonzero components per column. If k < n, this is usually not the same solution as pinv(A)*B, which is the least squares solution with the smallest norm 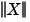 . . |
|
Array left division. A.\B is the matrix with elements B(i,j)/A(i,j). A and B must have the same size, unless one of them is a scalar. |
|
Matrix power. X^p is X to the power p, if p is a scalar. If p is an integer, the power is computed by repeated squaring. If the integer is negative, X is inverted first. For other values of p, the calculation involves eigenvalues and eigenvectors, such that if [V,D] = eig(X), then X^p = V*D.^p/V. |
|
If x is a scalar and P is a matrix, x^P is x raised to the matrix power P using eigenvalues and eigenvectors. X^P, where X and P are both matrices, is an error. |
|
Array power. A.^B is the matrix with elements A(i,j) to the B(i,j) power. A and B must have the same size, unless one of them is a scalar. |
|
Matrix transpose. A' is the linear algebraic transpose of A. For complex matrices, this is the complex conjugate transpose. |
|
Array transpose. A.' is the array transpose of A. For complex matrices, this does not involve conjugation. |
This section describes the arithmetic operators' support for data types other than double.
Data Type single
You can apply any of the arithmetic operators to arrays of type single and MATLAB returns an answer of type single. You can also combine an array of type double with an array of type single, and the result has type single.
Integer Data Types
You can apply most of the arithmetic operators to real arrays of the following integer data types:
All operands must have the same integer data type and MATLAB returns an answer of that type.
The following table lists the binary arithmetic operators that you can apply to arrays of the same integer data type. In the table, A and B are arrays of the same integer data type and c is a scalar of type double or the same type as A and B.
Combining Integer Data Types with Type Double
For the operations that support integer data types, you can combine a scalar or array of an integer data type with a scalar, but not an array, of type double and the result has the same integer data type as the input of integer type. For example,
However, you cannot combine an array of an integer data type with either of the following:
Nondouble Data Types, in the online MATLAB documentation, provides more information about operations on nondouble data types.
Remarks
The arithmetic operators have M-file function equivalents, as shown:
Examples
Here are two vectors, and the results of various matrix and array operations on them, printed with format rat.
Diagnostics
A is singular,
A is rank deficient,
See Also
mldivide, mrdivide, chol, det, inv, lu, orth, permute, ipermute, qr, rref
References
[1] Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide (http://www.netlib.org/lapack/lug/lapack_lug.html), Third Edition, SIAM, Philadelphia, 1999.
[2] Davis, T.A., UMFPACK Version 4.0 User Guide (http://www.cise.ufl.edu/research/sparse/umfpack/v4.0/UserGuide.pdf), Dept. of Computer and Information Science and Engineering, Univ. of Florida, Gainesville, FL, 2002.
 | wait | Relational Operators < > <= >= == ~= |  |
© 1994-2005 The MathWorks, Inc.