lu (MATLAB Functions)

LU matrix factorization

Syntax

[L,U] = lu(X)
[L,U,P] = lu(X)
Y = lu(X)
[L,U,P,Q] = lu(X)
[L,U,P] = lu(X,thresh)
[L,U,P,Q] = lu(X,thresh)

Description

The lu function expresses a matrix X as the product of two essentially triangular matrices, one of them a permutation of a lower triangular matrix and the other an upper triangular matrix. The factorization is often called the LU, or sometimes the LR, factorization. X can be rectangular. For a full matrix X, lu uses the Linear Algebra Package (LAPACK) routines described in Algorithm.

[L,U] = lu(X) returns an upper triangular matrix in U and a permuted lower triangular matrix L (that is, a product of lower triangular and permutation matrices), such that X = L*U.

[L,U,P] = lu(X) returns an upper triangular matrix in U, a lower triangular matrix L with a unit diagonal, and a permutation matrix P, so that L*U = P*X.

Y = lu(X) returns a matrix Y, which contains the strictly lower triangular L, i.e., without its unit diagonal, and the upper triangular U as submatrices. That is, if [L,U,P] = lu(X), then Y = U+L-eye(size(X)). The permutation matrix P is not returned by Y = lu(X).

[L,U,P,Q] = lu(X) for sparse nonempty X, returns a unit lower triangular matrix L, an upper triangular matrix U, a row permutation matrix P, and a column reordering matrix Q, so that P*X*Q = L*U. This syntax uses UMFPACK and is significantly more time and memory efficient than the other syntaxes, even when used with colamd. If X is empty or not sparse, lu displays an error message.

[L,U,P] = lu(X,thresh) controls pivoting in sparse matrices, where thresh is a pivot threshold in the interval [0,1]. Pivoting occurs when the diagonal entry in a column has magnitude less than thresh times the magnitude of any sub-diagonal entry in that column. thresh = 0 forces diagonal pivoting. thresh = 1 (conventional partial pivoting) is the default.

[L,U,P,Q] = lu(X,thresh) controls pivoting in UMFPACK, where thresh is a pivot threshold in the interval [0,1]. Given a pivot column j, UMFPACK selects the sparsest candidate pivot row i such that the absolute value of the pivot entry is greater than or equal to thresh times the absolute value of the largest entry in the column j. For complex matrices, absolute values are computed as abs(real(a)) + abs(imag(a)). The magnitude of entries in L is limited to 1/thresh.

Setting thresh to 1.0 results in conventional partial pivoting. The default value is 0.1. Smaller values of thresh lead to sparser LU factors, but the solution might be inaccurate. Larger values usually (but not always) lead to a more accurate solution, but increase the number of steps the algorithm performs.

Note In rare instances, incorrect factorization results in P*X*Q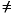

L*U. Increase thresh, to a maximum of 1.0 (regular partial pivoting), and try again.

Remarks

Most of the algorithms for computing LU factorization are variants of Gaussian elimination. The factorization is a key step in obtaining the inverse with inv and the determinant with det. It is also the basis for the linear equation solution or matrix division obtained with \ and /.

Arguments

X
Rectangular matrix to be factored.

thresh
Pivot threshold for sparse matrices. Valid values are in the interval [0,1]. If you specify the fourth output Q, the default is 0.1. Otherwise the default is 1.0.

L
Factor of X. Depending on the form of the function, L is either a unit lower triangular matrix, or else the product of a unit lower triangular matrix with P'.

U
Upper triangular matrix that is a factor of X.

P
Row permutation matrix satisfying the equation L*U = P*X, or L*U = P*X*Q. Used for numerical stability.

Q
Column permutation matrix satisfying the equation P*X*Q = L*U. Used to reduce fill-in in the sparse case.

`X`	Rectangular matrix to be factored.
`thresh`	Pivot threshold for sparse matrices. Valid values are in the interval `[0,1]`. If you specify the fourth output `Q`, the default is `0.1`. Otherwise the default is `1.0`.
`L`	Factor of `X`. Depending on the form of the function, `L` is either a unit lower triangular matrix, or else the product of a unit lower triangular matrix with `P'`.
`U`	Upper triangular matrix that is a factor of `X`.
`P`	Row permutation matrix satisfying the equation `LU = PX`, or `LU = PX*Q`. Used for numerical stability.
`Q`	Column permutation matrix satisfying the equation `PXQ = L*U`. Used to reduce fill-in in the sparse case.

Examples

Example 1. Start with

A = [ 1    2    3
      4    5    6
      7    8    0 ];

To see the LU factorization, call lu with two output arguments.

[L1,U] = lu(A)

L1 =
    0.1429    1.0000         0
    0.5714    0.5000    1.0000
    1.0000         0         0

U =
    7.0000    8.0000         0
         0    0.8571    3.0000
         0         0    4.5000

Notice that L1 is a permutation of a lower triangular matrix: if you switch rows 2 and 3, and then switch rows 1 and 2, the resulting matrix is lower triangular and has 1s on the diagonal. Notice also that U is upper triangular. To check that the factorization does its job, compute the product

```
L1*U
```

which returns the original A. The inverse of the example matrix, X = inv(A), is actually computed from the inverses of the triangular factors

```
X = inv(U)*inv(L1)
```

Using three arguments on the left side to get the permutation matrix as well

```
[L2,U,P] = lu(A)
```

returns a truly lower triangular L2, the same value of U, and the permutation matrix P.

L2 =

    1.0000         0         0
    0.1429    1.0000         0
    0.5714    0.5000    1.0000

U =
    7.0000    8.0000         0
         0    0.8571    3.0000
         0         0    4.5000

P =
    0    0    1
    1    0    0
    0    1    0

Note that L2 = P*L1.

P*L1

ans =

    1.0000         0         0
    0.1429    1.0000         0
    0.5714    0.5000    1.0000

To verify that L2*U is a permuted version of A, compute L2*U and subtract it from P*A:

P*A - L2*U

ans =
     0     0     0
     0     0     0
     0     0     0

In this case, inv(U)*inv(L) results in the permutation of inv(A) given by inv(P)*inv(A).

The determinant of the example matrix is

```
d = det(A)

d =
    27
```

It is computed from the determinants of the triangular factors

```
d = det(L)*det(U)
```

The solution to 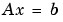is obtained with matrix division

```
x = A\b
```

The solution is actually computed by solving two triangular systems

```
y = L\b
x = U\y
```

Example 2. Generate a 60-by-60 sparse adjacency matrix of the connectivity graph of the Buckminster-Fuller geodesic dome.

```
B = bucky;
```

Use the sparse matrix syntax with four outputs to get the row and column permutation matrices.

```
[L,U,P,Q] = lu(B);
```

Apply the permutation matrices to B, and subtract the product of the lower and upper triangular matrices.

Z = P*B*Q - L*U;
norm(Z,1)

ans =
  7.9936e-015

The 1-norm of their difference is within roundoff error, indicating that L*U = P*B*Q.

Algorithm

For full matrices X, lu uses the LAPACK routines listed in the following table.

Real
Complex

X double
DGETRF
ZGETRF

X single
SGETRF
CGETRF

	Real	Complex
`X` `double`	DGETRF	ZGETRF
`X` `single`	SGETRF	CGETRF

For sparse X, with four outputs, lu uses UMFPACK routines. With three or fewer outputs, lu uses its own sparse matrix routines.

See Also

cond, det, inv, luinc, qr, rref

The arithmetic operators \ and /

References

[1] Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide (http://www.netlib.org/lapack/lug/lapack_lug.html), Third Edition, SIAM, Philadelphia, 1999.

[2] Davis, T. A., UMFPACK Version 4.0 User Guide (http://www.cise.ufl.edu/research/sparse/umfpack/v4.0/UserGuide.pdf), Dept. of Computer and Information Science and Engineering, Univ. of Florida, Gainesville, FL, 2002.

lt luinc