cholupdate (MATLAB Functions)

Rank 1 update to Cholesky factorization

Syntax

R1 = cholupdate(R,x)
R1 = cholupdate(R,x,'+')
R1 = cholupdate(R,x,'-')
[R1,p] = cholupdate(R,x,'-')

Description

R1 = cholupdate(R,x) where R = chol(A) is the original Cholesky factorization of A, returns the upper triangular Cholesky factor of A + x*x', where x is a column vector of appropriate length. cholupdate uses only the diagonal and upper triangle of R. The lower triangle of R is ignored.

R1 = cholupdate(R,x,'+') is the same as R1 = cholupdate(R,x).

R1 = cholupdate(R,x,'-') returns the Cholesky factor of A - x*x'. An error message reports when R is not a valid Cholesky factor or when the downdated matrix is not positive definite and so does not have a Cholesky factorization.

[R1,p] = cholupdate(R,x,'-') will not return an error message. If p is 0, R1 is the Cholesky factor of A - x*x'. If p is greater than 0, R1 is the Cholesky factor of the original A. If p is 1, cholupdate failed because the downdated matrix is not positive definite. If p is 2, cholupdate failed because the upper triangle of R was not a valid Cholesky factor.

Remarks

cholupdate works only for full matrices.

Example

A = pascal(4)
A =

     1     1     1     1
     1     2     3     4
     1     3     6    10
     1     4    10    20

R = chol(A)
R =

     1     1     1     1
     0     1     2     3
     0     0     1     3
     0     0     0     1
x = [0 0 0 1]';

This is called a rank one update to A since rank(x*x') is 1:

```
A + x*x' 
ans =
```

     1     1     1     1
     1     2     3     4
     1     3     6    10
     1     4    10    21

Instead of computing the Cholesky factor with R1 = chol(A + x*x'), we can use cholupdate:

```
R1 = cholupdate(R,x)
R1 =
```

    1.0000    1.0000    1.0000    1.0000
         0    1.0000    2.0000    3.0000
         0         0    1.0000    3.0000
         0         0         0    1.4142

Next destroy the positive definiteness (and actually make the matrix singular) by subtracting 1 from the last element of A. The downdated matrix is:

A - x*x'
ans =
 
     1     1     1     1
     1     2     3     4
     1     3     6    10
     1     4    10    19

Compare chol with cholupdate:

R1 = chol(A-x*x')
??? Error using ==> chol
Matrix must be positive definite.
R1 = cholupdate(R,x,'-')
??? Error using ==> cholupdate
Downdated matrix must be positive definite.

However, subtracting 0.5 from the last element of A produces a positive definite matrix, and we can use cholupdate to compute its Cholesky factor:

x = [0 0 0 1/sqrt(2)]';
R1 = cholupdate(R,x,'-') 
R1 =
    1.0000    1.0000    1.0000    1.0000
         0    1.0000    2.0000    3.0000
         0         0    1.0000    3.0000
         0         0         0    0.7071

Algorithm

cholupdate uses the algorithms from the LINPACK subroutines ZCHUD and ZCHDD. cholupdate is useful since computing the new Cholesky factor from scratch is an 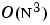algorithm, while simply updating the existing factor in this way is an 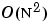algorithm.

See Also

chol, qrupdate

References

[1] Dongarra, J.J., J.R. Bunch, C.B. Moler, and G.W. Stewart, LINPACK Users' Guide, SIAM, Philadelphia, 1979.

cholinc circshift