qrupdate (MATLAB Functions)

qrupdate
Description

Rank 1 update to QR factorization

Syntax

```
[Q1,R1] = qrupdate(Q,R,u,v)
```

Description

[Q1,R1] = qrupdate(Q,R,u,v) when [Q,R] = qr(A) is the original QR factorization of A, returns the QR factorization of A + u*v', where u and v are column vectors of appropriate lengths.

Remarks

qrupdate works only for full matrices.

Examples

The matrix

mu = sqrt(eps)

mu =

   1.4901e-08

A = [ones(1,4); mu*eye(4)];

is a well-known example in least squares that indicates the dangers of forming A'*A. Instead, we work with the QR factorization - orthonormal Q and upper triangular R.

```
 [Q,R] = qr(A);
```

As we expect, R is upper triangular.

R =

   -1.0000   -1.0000   -1.0000   -1.0000
         0    0.0000    0.0000    0.0000
         0         0    0.0000    0.0000
         0         0         0    0.0000
         0         0         0         0

In this case, the upper triangular entries of R, excluding the first row, are on the order of sqrt(eps).

Consider the update vectors

```
 u = [-1 0 0 0 0]'; v = ones(4,1);
```

Instead of computing the rather trivial QR factorization of this rank one update to A from scratch with

[QT,RT] = qr(A + u*v')

QT =

     0     0     0     0     1
    -1     0     0     0     0
     0    -1     0     0     0
     0     0    -1     0     0
     0     0     0    -1     0

RT =

  1.0e-007 *

   -0.1490         0         0         0
         0   -0.1490         0         0
         0         0   -0.1490         0
         0         0         0   -0.1490
         0         0         0         0

we may use qrupdate.

[Q1,R1] = qrupdate(Q,R,u,v)

Q1 =

   -0.0000   -0.0000   -0.0000   -0.0000    1.0000
    1.0000   -0.0000   -0.0000   -0.0000    0.0000
    0.0000    1.0000   -0.0000   -0.0000    0.0000
    0.0000    0.0000    1.0000   -0.0000    0.0000
   -0.0000   -0.0000   -0.0000    1.0000    0.0000

R1 =

   1.0e-007 *
    0.1490    0.0000    0.0000    0.0000
         0    0.1490    0.0000    0.0000
         0         0    0.1490    0.0000
         0         0         0    0.1490
         0         0         0         0

Note that both factorizations are correct, even though they are different.

Algorithm

qrupdate uses the algorithm in section 12.5.1 of the third edition of Matrix Computations by Golub and van Loan. qrupdate is useful since, if we take N = max(m,n), then computing the new QR factorization from scratch is roughly an 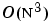algorithm, while simply updating the existing factors in this way is an 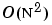algorithm.

References

[1] Golub, Gene H. and Charles Van Loan, Matrix Computations, Third Edition, Johns Hopkins University Press, Baltimore, 1996

See Also

cholupdate, qr

qrinsert quad, quad8