corrcoef (MATLAB Functions)

Correlation coefficients

Syntax

R = corrcoef(X)
R = corrcoef(x,y)
[R,P]=corrcoef(...)
[R,P,RLO,RUP]=corrcoef(...)
[...]=corrcoef(...,'param1',val1,'param2',val2,...)

Description

R = corrcoef(X) returns a matrix R of correlation coefficients calculated from an input matrix X whose rows are observations and whose columns are variables. The matrix R = corrcoef(X) is related to the covariance matrix C = cov(X) by

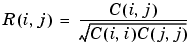
corrcoef(X) is the zeroth lag of the normalized covariance function, that is, the zeroth lag of xcov(x,'coeff') packed into a square array.

R = corrcoef(x,y) where x and y are column vectors is the same as corrcoef([x y]).

[R,P]=corrcoef(...) also returns P, a matrix of p-values for testing the hypothesis of no correlation. Each p-value is the probability of getting a correlation as large as the observed value by random chance, when the true correlation is zero. If P(i,j) is small, say less than 0.05, then the correlation R(i,j) is significant.

[R,P,RLO,RUP]=corrcoef(...) also returns matrices RLO and RUP, of the same size as R, containing lower and upper bounds for a 95% confidence interval for each coefficient.

[...]=corrcoef(...,'param1',val1,'param2',val2,...) specifies additional parameters and their values. Valid parameters are the following.

'alpha'
A number between 0 and 1 to specify a confidence level of 100*(1 - alpha)%. Default is 0.05 for 95% confidence intervals.

'rows'
Either 'all' (default) to use all rows, 'complete' to use rows with no NaN values, or 'pairwise' to compute R(i,j) using rows with no NaN values in either column i or j.

`'alpha'`	A number between 0 and 1 to specify a confidence level of 100*(1 - `alpha`)%. Default is 0.05 for 95% confidence intervals.
`'rows'`	Either `'all'` (default) to use all rows, `'complete'` to use rows with no `NaN` values, or `'pairwise'` to compute `R(i,j)` using rows with no `NaN` values in either column `i` or `j`.

The p-value is computed by transforming the correlation to create a t statistic having n-2 degrees of freedom, where n is the number of rows of X. The confidence bounds are based on an asymptotic normal distribution of 0.5*log((1+R)/(1-R)), with an approximate variance equal to 1/(n-3). These bounds are accurate for large samples when X has a multivariate normal distribution. The 'pairwise' option can produce an R matrix that is not positive definite.

Examples

Generate random data having correlation between column 4 and the other columns.

x = randn(30,4);     % Uncorrelated data
x(:,4) = sum(x,2);   % Introduce correlation.
[r,p] = corrcoef(x)  % Compute sample correlation and p-values.
[i,j] = find(p<0.05);  % Find significant correlations.
[i,j]                % Display their (row,col) indices.

r =
    1.0000   -0.3566    0.1929    0.3457
   -0.3566    1.0000   -0.1429    0.4461
    0.1929   -0.1429    1.0000    0.5183
    0.3457    0.4461    0.5183    1.0000

p =
    1.0000    0.0531    0.3072    0.0613
    0.0531    1.0000    0.4511    0.0135
    0.3072    0.4511    1.0000    0.0033
    0.0613    0.0135    0.0033    1.0000

ans =
     4     2
     4     3
     2     4
     3     4

See Also

cov, mean, median, std, var

xcorr, xcov in the Signal Processing Toolbox

copyobj cos