cov (MATLAB Functions)

Covariance matrix

Syntax

```
C = cov(X)
C = cov(x,y)
```

Description

cov(X), if X is a vector, returns the variance. For matrices, where each row is an observation, and each column is a variable, cov(X) is the covariance matrix. diag(cov(X)) is a vector of variances for each column, and sqrt(diag(cov(X))) is a vector of standard deviations. cov(X,Y), where X and Y are vectors of equal length, is equivalent to cov([X(:) Y(:)]).

cov(X) or cov(X,Y) normalizes by N-1 where N is the number of observations. This makes cov(X) the best unbiased estimate of the covariance matrix if the observations are from a normal distribution.

cov(X,1) or cov(X,Y,1) normalizes by N and produces the second moment matrix of the observations about their mean. cov(X,Y,0) is the same as cov(X,Y) and cov(X,0) is the same as cov(X).

Remarks

cov removes the mean from each column before calculating the result.

The covariance function is defined as

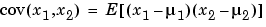
where 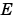is the mathematical expectation and .

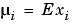Examples

Consider A = [-1 1 2 ; -2 3 1 ; 4 0 3]. To obtain a vector of variances for each column of A:

v = diag(cov(A))'
v =
   10.3333    2.3333    1.0000

Compare vector v with covariance matrix C:

C =
   10.3333   -4.1667    3.0000
   -4.1667    2.3333   -1.5000
    3.0000   -1.5000    1.0000

The diagonal elements C(i,i) represent the variances for the columns of A. The off-diagonal elements C(i,j) represent the covariances of columns i and j.

See Also

corrcoef, mean, median, std, var

xcorr, xcov in the Signal Processing Toolbox

coth cplxpair