erf, erfc, erfcx, erfinv, erfcinv (MATLAB Functions)

Error functions

Syntax

Y = erf(X)             Error function
Y = erfc(X)            Complementary error function
Y = erfcx(X)           Scaled complementary error function
X = erfinv(Y)          Inverse error function
X = erfcinv(Y)         Inverse complementary error function

Definition

The error function erf(X) is twice the integral of the Gaussian distribution with 0 mean and variance of .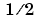

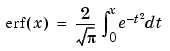
The complementary error function erfc(X) is defined as

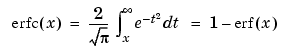
The scaled complementary error function erfcx(X) is defined as

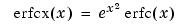
For large X, erfcx(X) is approximately

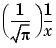
Description

Y = erf(X) returns the value of the error function for each element of real array X.

Y = erfc(X) computes the value of the complementary error function.

Y = erfcx(X) computes the value of the scaled complementary error function.

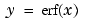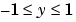X = erfinv(Y) returns the value of the inverse error function for each element of Y. Elements of Y must be in the interval [-1 1]. The function erfinv satisfies for and .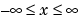

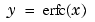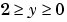X = erfcinv(Y) returns the value of the inverse of the complementary error function for each element of Y. Elements of Y must be in the interval [0 2]. The function erfcinv satisfies for and .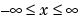

Remarks

The relationship between the complementary error function erfc and the standard normal probability distribution returned by the Statistics Toolbox function normcdf is

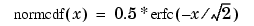
The relationship between the inverse complementary error function erfcinv and the inverse standard normal probability distribution returned by the Statistics Toolbox function norminv is

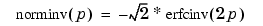
Examples

erfinv(1) is Inf

erfinv(-1) is -Inf.

For abs(Y) > 1, erfinv(Y) is NaN.

Algorithms

For the error functions, the MATLAB code is a translation of a Fortran program by W. J. Cody, Argonne National Laboratory, NETLIB/SPECFUN, March 19, 1990. The main computation evaluates near-minimax rational approximations from [1].

For the inverse of the error function, rational approximations accurate to approximately six significant digits are used to generate an initial approximation, which is then improved to full accuracy by one step of Halley's method.

References

[1] Cody, W. J., "Rational Chebyshev Approximations for the Error Function," Math. Comp., pgs. 631-638, 1969

eq error