fft (MATLAB Functions)

Discrete Fourier transform

Syntax

Y = fft(X)
Y = fft(X,n)
Y = fft(X,[],dim)
Y = fft(X,n,dim)

Definition

The functions X = fft(x) and x = ifft(X) implement the transform and inverse transform pair given for vectors of length 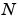by:

where

is an th root of unity.

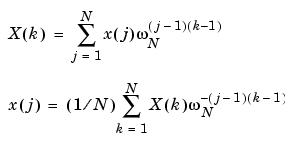
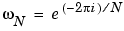
Description

Y = fft(X) returns the discrete Fourier transform (DFT) of vector X, computed with a fast Fourier transform (FFT) algorithm.

If X is a matrix, fft returns the Fourier transform of each column of the matrix.

If X is a multidimensional array, fft operates on the first nonsingleton dimension.

Y = fft(X,n) returns the n-point DFT. If the length of X is less than n, X is padded with trailing zeros to length n. If the length of X is greater than n, the sequence X is truncated. When X is a matrix, the length of the columns are adjusted in the same manner.

Y = fft(X,[],dim) and Y = fft(X,n,dim) applies the FFT operation across the dimension dim.

Examples

A common use of Fourier transforms is to find the frequency components of a signal buried in a noisy time domain signal. Consider data sampled at 1000 Hz. Form a signal containing 50 Hz and 120 Hz and corrupt it with some zero-mean random noise:

t = 0:0.001:0.6;
x = sin(2*pi*50*t)+sin(2*pi*120*t);
y = x + 2*randn(size(t));
plot(1000*t(1:50),y(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')

It is difficult to identify the frequency components by looking at the original signal. Converting to the frequency domain, the discrete Fourier transform of the noisy signal y is found by taking the 512-point fast Fourier transform (FFT):

```
Y = fft(y,512);
```

The power spectrum, a measurement of the power at various frequencies, is

```
Pyy = Y.* conj(Y) / 512;
```

Graph the first 257 points (the other 255 points are redundant) on a meaningful frequency axis:

f = 1000*(0:256)/512;
plot(f,Pyy(1:257))
title('Frequency content of y')
xlabel('frequency (Hz)')

This represents the frequency content of y in the range from DC up to and including the Nyquist frequency. (The signal produces the strong peaks.)

Algorithm

The FFT functions (fft, fft2, fftn, ifft, ifft2, ifftn) are based on a library called FFTW [3],[4]. To compute an 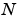-point DFT when 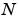is composite (that is, when 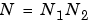), the FFTW library decomposes the problem using the Cooley-Tukey algorithm [1], which first computes 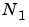transforms of size 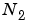, and then computes 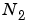transforms of size 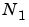. The decomposition is applied recursively to both the 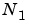- and 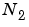-point DFTs until the problem can be solved using one of several machine-generated fixed-size "codelets." The codelets in turn use several algorithms in combination, including a variation of Cooley-Tukey [5], a prime factor algorithm [6], and a split-radix algorithm [2]. The particular factorization of 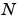is chosen heuristically.

When 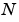is a prime number, the FFTW library first decomposes an 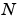-point problem into three (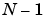)-point problems using Rader's algorithm [7]. It then uses the Cooley-Tukey decomposition described above to compute the (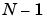)-point DFTs.

For most 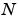, real-input DFTs require roughly half the computation time of complex-input DFTs. However, when 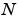has large prime factors, there is little or no speed difference.

The execution time for fft depends on the length of the transform. It is fastest for powers of two. It is almost as fast for lengths that have only small prime factors. It is typically several times slower for lengths that are prime or which have large prime factors.

Note You might be able to increase the speed of fft using the utility function fftw, which controls how MATLAB optimizes the algorithm used to compute an FFT of a particular size and dimension.

Data Type Support

fft supports inputs of data types double and single. If you call fft with the syntax y = fft(X, ...), the output y has the same data type as the input X.

See Also

fft2, fftn, fftw, fftshift, ifft

dftmtx, filter, and freqz in the Signal Processing Toolbox

References

[1] Cooley, J. W. and J. W. Tukey, "An Algorithm for the Machine Computation of the Complex Fourier Series," Mathematics of Computation, Vol. 19, April 1965, pp. 297-301.

[2] Duhamel, P. and M. Vetterli, "Fast Fourier Transforms: A Tutorial Review and a State of the Art," Signal Processing, Vol. 19, April 1990, pp. 259-299.

[3] FFTW (http://www.fftw.org)

[4] Frigo, M. and S. G. Johnson, "FFTW: An Adaptive Software Architecture for the FFT," Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Vol. 3, 1998, pp. 1381-1384.

[5] Oppenheim, A. V. and R. W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, p. 611.

[6] Oppenheim, A. V. and R. W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, p. 619.

[7] Rader, C. M., "Discrete Fourier Transforms when the Number of Data Samples Is Prime," Proceedings of the IEEE, Vol. 56, June 1968, pp. 1107-1108.

feval fft2