fminbnd (MATLAB Functions)

Minimize a function of one variable on a fixed interval

Syntax

x = fminbnd(fun,x1,x2)
x = fminbnd(fun,x1,x2,options)
[x,fval] = fminbnd(...)
[x,fval,exitflag] = fminbnd(...)
[x,fval,exitflag,output] = fminbnd(...)

Description

fminbnd finds the minimum of a function of one variable within a fixed interval.

x = fminbnd(fun,x1,x2) returns a value x that is a local minimizer of the function that is described in fun in the interval x1 <= x <= x2. fun is a function handle. See Function Handles in the MATLAB Programming documentation for more information.

Parameterizing Functions Called by Function Functions, in the MATLAB mathematics documentation, explains how to provide additional parameters to the function fun, if necessary.

x = fminbnd(fun,x1,x2,options) minimizes with the optimization parameters specified in the structure options. You can define these parameters using the optimset function. fminbnd uses these options structure fields:

Display
Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' displays just the final output; 'notify' (default) displays output only if the function does not converge.

FunValCheck
Check whether objective function values are valid. 'on' displays a warning when the objective function returns a value that is complex or NaN. 'off' displays no warning.

MaxFunEvals
Maximum number of function evaluations allowed.

MaxIter
Maximum number of iterations allowed.

OutputFcn
Specify a user-defined function that the optimization function calls at each iteration.

TolX
Termination tolerance on x.

`Display`	Level of display. `'off'` displays no output; `'iter'` displays output at each iteration; `'final'` displays just the final output; `'notify'` (default) displays output only if the function does not converge.
`FunValCheck`	Check whether objective function values are valid. `'on'` displays a warning when the objective function returns a value that is `complex` or `NaN`. `'off'` displays no warning.
`MaxFunEvals`	Maximum number of function evaluations allowed.
`MaxIter`	Maximum number of iterations allowed.
`OutputFcn`	Specify a user-defined function that the optimization function calls at each iteration.
`TolX`	Termination tolerance on `x`.

[x,fval] = fminbnd(...) returns the value of the objective function computed in fun at x.

[x,fval,exitflag] = fminbnd(...) returns a value exitflag that describes the exit condition of fminbnd:

1
fminbnd converged to a solution x based on options.TolX.

0
Maximum number of function evaluations or iterations was reached.

-1
Algorithm was terminated by the output function.

-2
Bounds are inconsistent (ax > bx).

`1`	`fminbnd` converged to a solution `x` based on `options.TolX.`
`0`	Maximum number of function evaluations or iterations was reached.
`-1`	Algorithm was terminated by the output function.
`-2`	Bounds are inconsistent (`ax > bx`).

[x,fval,exitflag,output] = fminbnd(...) returns a structure output that contains information about the optimization:

output.algorithm
Algorithm used

output.funcCount
Number of function evaluations

output.iterations
Number of iterations

output.message
Exit message

`output.algorithm`	Algorithm used
`output.funcCount`	Number of function evaluations
`output.iterations`	Number of iterations
`output.message`	Exit message

Arguments

fun is the function to be minimized. fun accepts a scalar x and returns a scalar f, the objective function evaluated at x. The function fun can be specified as a function handle for an M-file function

```
x = fminbnd(@myfun,x1,x2);
```

where myfun.m is an M-file function such as

function f = myfun(x)
f = ...         % Compute function value at x.

or as a function handle for an anonymous function:

```
x = fminbnd(@(x) sin(x*x),x1,x2);
```

Other arguments are described in the syntax descriptions above.

Examples

x = fminbnd(@cos,3,4) computes 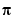to a few decimal places and gives a message on termination.

[x,fval,exitflag] = ...
   fminbnd(@cos,3,4,optimset('TolX',1e-12,'Display','off'))

computes 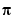to about 12 decimal places, suppresses output, returns the function value at x, and returns an exitflag of 1.

The argument fun can also be a function handle for an anonymous function. For example, to find the minimum of the function 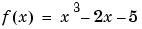on the interval (0,2), create an anonymous function f

```
f = @(x)x.^3-2*x-5;
```

Then invoke fminbnd with

```
x = fminbnd(f, 0, 2)
```

The result is

```
x =
    0.8165
```

The value of the function at the minimum is

```
y = f(x)

y =
    -6.0887
```

If fun is parameterized, you can use anonymous functions to capture the problem-dependent parameters. For example, suppose you want to minimize the objective function myfun defined by the following M-file function.

```
function f = myfun(x,a)
f = (x - a)^2;
```

Note that myfun has an extra parameter a, so you cannot pass it directly to fminbind. To optimize for a specific value of a, such as a = 1.5.

Assign the value to a.

```
a = 1.5; % define parameter first
```

Call fminbnd with a one-argument anonymous function that captures that value of a and calls myfun with two arguments:

```
x = fminbnd(@(x) myfun(x,a),0,1)
```

Algorithm

fminbnd is an M-file. The algorithm is based on golden section search and parabolic interpolation. Unless the left endpoint x₁ is very close to the right endpoint x₂, fminbnd never evaluates fun at the endpoints, so fun need only be defined for x in the interval x₁ < x < x₂. If the minimum actually occurs at x₁ or x₂, fminbnd returns an interior point at a distance of no more than 2*TolX from x₁ or x₂, where TolX is the termination tolerance. See [1] or [2] for details about the algorithm.

Limitations

The function to be minimized must be continuous. fminbnd may only give local solutions.

fminbnd often exhibits slow convergence when the solution is on a boundary of the interval.

fminbnd only handles real variables.

References

[1] Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.

[2] Brent, Richard. P., Algorithms for Minimization without Derivatives, Prentice-Hall, Englewood Cliffs, New Jersey, 1973

flow fminsearch