

| MATLAB Function Reference |   |
Reorder eigenvalues in QZ factorization
Syntax
[AAS,BBS,QS,ZS] = ordqz(AA,BB,Q,Z,select) [...] = ordqz(AA,BB,Q,Z,keyword) [...] = ordqz(AA,BB,Q,Z,clusters)
Description
[AAS,BBS,QS,ZS] = ordqz(AA,BB,Q,Z,select)
reorders the QZ factorizations Q*A*Z = AA and Q*B*Z = BB produced by the qz function for a matrix pair (A,B). It returns the reordered pair (AAS,BBS) and the cumulative orthogonal transformations QS and ZS such that QS*A*ZS = AAS and QS*B*ZS = BBS. In this reordering, the selected cluster of eigenvalues appears in the leading (upper left) diagonal blocks of the quasitriangular pair (AAS,BBS), and the corresponding invariant subspace is spanned by the leading columns of ZS. The logical vector select specifies the selected cluster as E(select) where E is the vector of eigenvalues as they appear along the diagonal of AA-.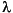 *BB
*BB
Note
To extract E from AA and BB, use ordeig(BB), instead of eig. This ensures that the eigenvalues in E occur in the same order as they appear on the diagonal of AA-.
|
[...] = ordqz(AA,BB,Q,Z,keyword)
sets the selected cluster to include all eigenvalues in the region specified by keyword:
| keyword |
Selected Region |
'lhp' |
Left-half plane (real(E) < 0) |
'rhp' |
Right-half plane (real(E) > 0) |
'udi' |
Interior of unit disk (abs(E) < 1) |
'udo' |
Exterior of unit disk (abs(E) > 1) |
[...] = ordqz(AA,BB,Q,Z,clusters)
reorders multiple clusters at once. Given a vector clusters of cluster indices commensurate with E = ordeig(AA,BB), such that all eigenvalues with the same clusters value form one cluster, ordqz sorts the specified clusters in descending order along the diagonal of (AAS,BBS). The cluster with highest index appears in the upper left corner.
Algorithm
For full matrices AA and BB, qz uses the LAPACK routines listed in the following table.
| AA and BB Real |
AA or BB Complex |
|
A and B double |
DTGSEN |
ZTGSEN |
A or B single |
STGSEN |
CTGSEN |
See Also
 | orderfields | ordschur |  |
© 1994-2005 The MathWorks, Inc.