

| MATLAB Function Reference |   |
Piecewise Cubic Hermite Interpolating Polynomial (PCHIP)
Syntax
Description
yi = pchip(x,y,xi)
returns vector yi containing elements corresponding to the elements of xi and determined by piecewise cubic interpolation within vectors x and y. The vector x specifies the points at which the data y is given. If y is a matrix, then the interpolation is performed for each column of y and yi is length(xi)-by-size(y,2).
pp = pchip(x,y)
returns a piecewise polynomial structure for use by ppval. x can be a row or column vector. y is a row or column vector of the same length as x, or a matrix with length(x) columns.
pchip finds values of an underlying interpolating function 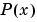 at intermediate points, such that:
at intermediate points, such that:
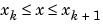 ,
, 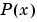 is the cubic Hermite interpolant to the given values and certain slopes at the two endpoints.
is the cubic Hermite interpolant to the given values and certain slopes at the two endpoints.
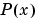 interpolates
interpolates 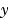 , i.e.,
, i.e., 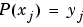 , and the first derivative
, and the first derivative 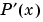 is continuous.
is continuous. 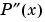 is probably not continuous; there may be jumps at the
is probably not continuous; there may be jumps at the 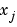 .
.
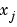 are chosen in such a way that
are chosen in such a way that 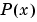 preserves the shape of the data and respects monotonicity. This means that, on intervals where the data are monotonic, so is
preserves the shape of the data and respects monotonicity. This means that, on intervals where the data are monotonic, so is 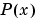 ; at points where the data has a local extremum, so does
; at points where the data has a local extremum, so does 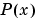 .
.
Remarks
spline constructs 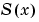 in almost the same way
in almost the same way pchip constructs 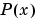 . However,
. However, spline chooses the slopes at the 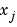 differently, namely to make even
differently, namely to make even 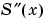 continuous. This has the following effects:
continuous. This has the following effects:
spline produces a smoother result, i.e. 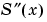 is continuous.
is continuous.
spline produces a more accurate result if the data consists of values of a smooth function.
pchip has no overshoots and less oscillation if the data are not smooth.
pchip is less expensive to set up.
Examples
x = -3:3; y = [-1 -1 -1 0 1 1 1]; t = -3:.01:3; p = pchip(x,y,t); s = spline(x,y,t); plot(x,y,'o',t,p,'-',t,s,'-.') legend('data','pchip','spline',4)
See Also
References
[1] Fritsch, F. N. and R. E. Carlson, "Monotone Piecewise Cubic Interpolation," SIAM J. Numerical Analysis, Vol. 17, 1980, pp.238-246.
[2] Kahaner, David, Cleve Moler, Stephen Nash, Numerical Methods and Software, Prentice Hall, 1988.
 | pcg | pcode |  |
© 1994-2005 The MathWorks, Inc.