polyfit (MATLAB Functions)

Polynomial curve fitting

Syntax

p = polyfit(x,y,n)
[p,S] = polyfit(x,y,n)
[p,S,mu] = polyfit(x,y,n)

Description

p = polyfit(x,y,n) finds the coefficients of a polynomial p(x) of degree n that fits the data, p(x(i)) to y(i), in a least squares sense. The result p is a row vector of length n+1 containing the polynomial coefficients in descending powers

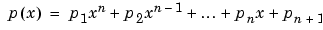
[p,S] = polyfit(x,y,n) returns the polynomial coefficients p and a structure S for use with polyval to obtain error estimates or predictions. If the errors in the data y are independent normal with constant variance, polyval produces error bounds that contain at least 50% of the predictions.

[p,S,mu] = polyfit(x,y,n) finds the coefficients of a polynomial in

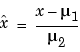
where 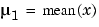and 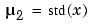. mu is the two-element vector 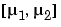. This centering and scaling transformation improves the numerical properties of both the polynomial and the fitting algorithm.

Examples

This example involves fitting the error function, erf(x), by a polynomial in x. This is a risky project because erf(x) is a bounded function, while polynomials are unbounded, so the fit might not be very good.

First generate a vector of x points, equally spaced in the interval 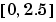; then evaluate erf(x) at those points.

```
x = (0: 0.1: 2.5)';
y = erf(x); 
```

The coefficients in the approximating polynomial of degree 6 are

p = polyfit(x,y,6)

p =

 0.0084  -0.0983   0.4217   -0.7435  0.1471   1.1064  0.0004

There are seven coefficients and the polynomial is

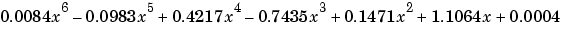
To see how good the fit is, evaluate the polynomial at the data points with

```
f = polyval(p,x); 
```

A table showing the data, fit, and error is

 table = [x y f y-f]
 
 table =

    0          0          0.0004    -0.0004
    0.1000     0.1125     0.1119     0.0006
    0.2000     0.2227     0.2223     0.0004
    0.3000     0.3286     0.3287    -0.0001
    0.4000     0.4284     0.4288    -0.0004
    ...
    2.1000     0.9970     0.9969     0.0001
    2.2000     0.9981     0.9982    -0.0001
    2.3000     0.9989     0.9991    -0.0003
    2.4000     0.9993     0.9995    -0.0002
    2.5000     0.9996     0.9994     0.0002

So, on this interval, the fit is good to between three and four digits. Beyond this interval the graph shows that the polynomial behavior takes over and the approximation quickly deteriorates.

x = (0: 0.1: 5)';
y = erf(x);
f = polyval(p,x);
plot(x,y,'o',x,f,'-')
axis([0  5  0  2])

Algorithm

The polyfit M-file forms the Vandermonde matrix, 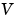, whose elements are powers of .

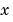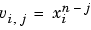
It then uses the backslash operator, \, to solve the least squares problem

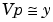
You can modify the M-file to use other functions of 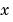as the basis functions.

See Also

poly, polyval, roots

polyeig polyint