polyeig (MATLAB Functions)

Polynomial eigenvalue problem

Syntax

[X,e] = polyeig(A0,A1,...Ap)
e = polyeig(A0,A1,..,Ap)
[X, e, s] = polyeig(A0,A1,..,AP)

Description

[X,e] = polyeig(A0,A1,...Ap) solves the polynomial eigenvalue problem of degree p

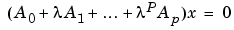
where polynomial degree p is a non-negative integer, and A0,A1,...Ap are input matrices of order n. The output consists of a matrix X, of size n-by-n*p, whose columns are the eigenvectors, and a vector e, of length n*p, containing the eigenvalues.

If lambda is the jth eigenvalue in e, and x is the jth column of eigenvectors in X, then (A0 + lambda*A1 + ... + lambda^p*Ap)*x is approximately 0.

e = polyeig(A0,A1,..,Ap) is a vector of length n*p whose elements are the eigenvalues of the polynomial eigenvalue problem.

[X, e, s] = polyeig(A0,A1,..,AP) also returns a p*n length vector s, of length p*n, containing condition numbers for the eigenvalues. At least one of A0 and AP must be nonsingular. Large condition numbers imply that the problem is close to a problem with multiple eigenvalues.

Remarks

Based on the values of p and n, polyeig handles several special cases:

p = 0, or polyeig(A) is the standard eigenvalue problem: eig(A).
p = 1, or polyeig(A,B) is the generalized eigenvalue problem: eig(A,-B).
n = 1, or polyeig(a0,a1,...ap) for scalars a0, a1 ..., ap is the standard polynomial problem: roots([ap ... a1 a0]).

If both A0 and Ap are singular the problem is potentially ill-posed. Theoretically, the solutions might not exist or might not be unique. Computationally, the computed solutions might be inaccurate. If one, but not both, of A0 and Ap is singular, the problem is well posed, but some of the eigenvalues might be zero or infinite.

Algorithm

The polyeig function uses the QZ factorization to find intermediate results in the computation of generalized eigenvalues. It uses these intermediate results to determine if the eigenvalues are well-determined. See the descriptions of eig and qz for more on this.

See Also

condeig, eig, qz

References

[1] Dedieu, Jean-Pierre Dedieu and Francoise Tisseur, "Perturbation theory for homogeneous polynomial eigenvalue problems," Linear Algebra Appl., Vol. 358, pp. 71-94, 2003.

[2] Tisseur, Francoise and Karl Meerbergen, "The quadratic eigenvalue problem," SIAM Rev., Vol. 43, Number 2, pp. 235-286, 2001.

polyder polyfit