quad, quad8 (MATLAB Functions)

Numerically evaluate integral, adaptive Simpson quadrature

Note The quad8 function, which implemented a higher order method, is obsolete. The quadl function is its recommended replacement.

Syntax

q = quad(fun,a,b)
q = quad(fun,a,b,tol)
q = quad(fun,a,b,tol,trace)
[q,fcnt] = quadl(fun,a,b,...)

Description

Quadrature is a numerical method used to find the area under the graph of a function, that is, to compute a definite integral.

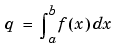
q = quad(fun,a,b) tries to approximate the integral of function fun from a to b to within an error of 1e-6 using recursive adaptive Simpson quadrature. fun is a function handle. See Function Handles in the MATLAB Programming documentation for more information. The function y = fun(x) should accept a vector argument x and return a vector result y, the integrand evaluated at each element of x.

Parameterizing Functions Called by Function Functions, in the MATLAB mathematics documentation, explains how to provide additional parameters to the function fun, if necessary.

q = quad(fun,a,b,tol) uses an absolute error tolerance tol instead of the default which is 1.0e-6. Larger values of tol result in fewer function evaluations and faster computation, but less accurate results. In MATLAB version 5.3 and earlier, the quad function used a less reliable algorithm and a default relative tolerance of 1.0e-3.

q = quad(fun,a,b,tol,trace) with non-zero trace shows the values of [fcnt a b-a Q] during the recursion.

[q,fcnt] = quad(...) returns the number of function evaluations.

The function quadl may be more efficient with high accuracies and smooth integrands.

Example

To compute the integral

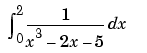
write an M-file function myfun that computes the integrand:

function y = myfun(x) 
y = 1./(x.^3-2*x-5);

Then pass @myfun, a function handle to myfun, to quad, along with the limits of integration, 0 to 2:

```
Q = quad(@myfun,0,2)

Q =

   -0.4605
```

Alternatively, you can pass the integrand to quad as an anonymous function handle F:

F = @(x)1./(x.^3-2*x-5);
Q = quad(F,0,2);

Algorithm

quad implements a low order method using an adaptive recursive Simpson's rule.

Diagnostics

quad may issue one of the following warnings:

'Minimum step size reached' indicates that the recursive interval subdivision has produced a subinterval whose length is on the order of roundoff error in the length of the original interval. A nonintegrable singularity is possible.

'Maximum function count exceeded' indicates that the integrand has been evaluated more than 10,000 times. A nonintegrable singularity is likely.

'Infinite or Not-a-Number function value encountered' indicates a floating point overflow or division by zero during the evaluation of the integrand in the interior of the interval.

References

[1] Gander, W. and W. Gautschi, "Adaptive Quadrature - Revisited", BIT, Vol. 40, 2000, pp. 84-101. This document is also available at http:// www.inf.ethz.ch/personal/gander.

qrupdate quadl