unwrap (MATLAB Functions)

Correct phase angles to produce smoother phase plots

Syntax

Q = unwrap(P)
Q = unwrap(P,tol)
Q = unwrap(P,[],dim)
Q = unwrap(P,tol,dim)

Description

Q = unwrap(P) corrects the radian phase angles in a vector P by adding multiples of 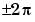when absolute jumps between consecutive elements of P are greater than the default jump tolerance of 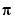radians. If P is a matrix, unwrap operates columnwise. If P is a multidimensional array, unwrap operates on the first nonsingleton dimension.

Q = unwrap(P,tol) uses a jump tolerance tol instead of the default value, .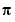

Q = unwrap(P,[],dim) unwraps along dim using the default tolerance.

Q = unwrap(P,tol,dim) uses a jump tolerance of tol.

Note A jump tolerance less than

has the same effect as a tolerance of

. For a tolerance less than

, if a jump is greater than the tolerance but less than

, adding

would result in a jump larger than the existing one, so unwrap chooses the current point. If you want to eliminate jumps that are less than

, try using a finer grid in the domain.

Examples

Example 1. The following phase data comes from the frequency response of a third-order transfer function. The phase curve jumps 3.5873 radians between w = 3.0 and w = 3.5, from -1.8621 to 1.7252.

w = [0:.2:3,3.5:1:10]; 
p = [    0
     -1.5728
     -1.5747
     -1.5772
     -1.5790
     -1.5816
     -1.5852
     -1.5877
     -1.5922
     -1.5976
     -1.6044
     -1.6129
     -1.6269
     -1.6512
     -1.6998
     -1.8621
      1.7252
      1.6124
      1.5930
      1.5916
      1.5708
      1.5708
      1.5708 ];
semilogx(w,p,'b*-'), hold

Using unwrap to correct the phase angle, the resulting jump is 2.6959, which is less than the default jump tolerance 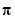. This figure plots the new curve over the original curve.

```
semilogx(w,unwrap(p),'r*-')
```

Note If you have the Control System Toolbox, you can create the data for this example with the following code.


   h = freqresp(tf(1,[1 .1 10 0]));
   p = angle(h(:));

Example 2. Array P features smoothly increasing phase angles except for discontinuities at elements (3,1) and (1,2).

P = [      0    7.0686    1.5708    2.3562
      0.1963    0.9817    1.7671    2.5525
      6.6759    1.1781    1.9635    2.7489
      0.5890    1.3744    2.1598    2.9452 ]

The function Q = unwrap(P) eliminates these discontinuities.

Q =
           0    7.0686    1.5708    2.3562
      0.1963    7.2649    1.7671    2.5525
      0.3927    7.4613    1.9635    2.7489
      0.5890    7.6576    2.1598    2.9452

See Also

abs, angle

untar unzip