Parametric Surfaces :: Creating 3-D Graphs (3-D Visualization)

3-D Visualization

Parametric Surfaces

The functions that draw surfaces can take two additional vector or matrix arguments to describe surfaces with specific x and y data. If Z is an m-by-n matrix, x is an n-vector, and y is an m-vector, then

```
mesh(x,y,Z,C)
```

describes a mesh surface with vertices having color C(i,j) and located at the points

```
(x(j), y(i), Z(i,j))
```

where x corresponds to the columns of Z and y to its rows.

More generally, if X, Y, Z, and C are matrices of the same dimensions, then

```
mesh(X,Y,Z,C)
```

describes a mesh surface with vertices having color C(i,j) and located at the points

```
(X(i,j), Y(i,j), Z(i,j))
```

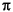
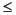
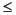
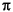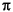
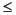
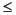
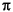
This example uses spherical coordinates to draw a sphere and color it with the pattern of pluses and minuses in a Hadamard matrix, an orthogonal matrix used in signal processing coding theory. The vectors theta and phi are in the range - theta and -/2 phi /2. Because theta is a row vector and phi is a column vector, the multiplications that produce the matrices X, Y, and Z are vector outer products.

k = 5;
n = 2^k-1;
theta = pi*(-n:2:n)/n;
phi = (pi/2)*(-n:2:n)'/n;
X = cos(phi)*cos(theta);
Y = cos(phi)*sin(theta);
Z = sin(phi)*ones(size(theta));
colormap([0 0 0;1 1 1])
C = hadamard(2^k);
surf(X,Y,Z,C)
axis square

Surface Plots of Nonuniformly Sampled Data Hidden Line Removal