Image Arithmetic :: Introduction (Image Processing Toolbox User's Guide)

Image Processing Toolbox User's Guide

Image Arithmetic

Image arithmetic is the implementation of standard arithmetic operations, such as addition, subtraction, multiplication, and division, on images. Image arithmetic has many uses in image processing both as a preliminary step in more complex operations and by itself. For example, image subtraction can be used to detect differences between two or more images of the same scene or object.

You can do image arithmetic using the MATLAB arithmetic operators. The Image Processing Toolbox also includes a set of functions that implement arithmetic operations for all numeric, nonsparse data types. The toolbox arithmetic functions accept any numeric data type, including uint8, uint16, and double, and return the result image in the same format. The functions perform the operations in double precision, on an element-by-element basis, but do not convert images to double-precision values in the MATLAB workspace. Overflow is handled automatically. The functions saturate return values to fit the data type. For details, see Image Arithmetic Saturation Rules.

Note On Intel architecture processors, the image arithmetic functions can take advantage of the Intel Performance Primitives Library (IPPL), thus accelerating their execution time. IPPL is only activated, however, when the data passed to these functions is of specific classes. See the reference pages for the individual arithmetic functions for more information.

Image Arithmetic Saturation Rules

The results of integer arithmetic can easily overflow the data type allotted for storage. For example, the maximum value you can store in uint8 data is 255. Arithmetic operations can also result in fractional values, which cannot be represented using integer arrays.

MATLAB arithmetic operators and the Image Processing Toolbox arithmetic functions use these rules for integer arithmetic:

Values that exceed the range of the integer type are saturated to that range.
Fractional values are rounded.

For example, if the data type is uint8, results greater than 255 (including Inf) are set to 255. The following table lists some additional examples.

Result
Class
Truncated Value

300
uint8
255

-45
uint8
0

10.5
uint8
11

Result	Class	Truncated Value
300	`uint8`	255
-45	`uint8`	0
10.5	`uint8`	11

Nesting Calls to Image Arithmetic Functions

You can use the image arithmetic functions in combination to perform a series of operations. For example, to calculate the average of two images,

You could enter

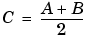
I = imread('rice.png');
I2 = imread('cameraman.tif');
K = imdivide(imadd(I,I2), 2); % not recommended

When used with uint8 or uint16 data, each arithmetic function rounds and saturates its result before passing it on to the next operation. This can significantly reduce the precision of the calculation. A better way to perform this calculation is to use the imlincomb function. imlincomb performs all the arithmetic operations in the linear combination in double precision and only rounds and saturates the final result.

K = imlincomb(.5,I,.5,I2); % recommended

Example: Creating a New Series Coordinate Systems