| Image Processing Toolbox User's Guide |
  |
Types of Supported Transformations
The cp2tform function can infer the parameters for six types of transformations. This table lists the transformations in order of complexity, with examples of each type of distortion.
The first four transformations, 'linear conformal', 'affine', 'projective', and 'polynomial' are global transformations. In these transformations, a single mathematical expression applies to an entire image. The last two transformations, 'piecewise linear' and 'lwm' (local weighted mean), are local transformations. In these transformations, different mathematical expressions apply to different regions within an image.
When exploring how different transformations affect the images you are working with, try the global transformations first. If these transformations are not satisfactory, try the local transformations: the piecewise linear transformation first and then the local weighted mean transformation.
Transformation Type
|
Description
|
Minimum Control Points
|
Example
|
'linear conformal'
|
Use this transformation when shapes in the input image are unchanged, but the image is distorted by some combination of translation, rotation, and scaling. Straight lines remain straight, and parallel lines are still parallel.
|
2 pairs
|

|
'affine'
|
Use this transformation when shapes in the input image exhibit shearing. Straight lines remain straight, and parallel lines remain parallel, but rectangles become parallelograms.
|
3 pairs
|

|
'projective'
|
Use this transformation when the scene appears tilted. Straight lines remain straight, but parallel lines converge toward vanishing points (which might or might not fall within the image).
|
4 pairs
|
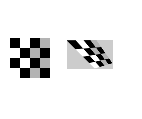
|
'polynomial'
|
Use this transformation when objects in the image are curved. The higher the order of the polynomial, the better the fit, but the result can contain more curves than the base image.
|
6 pairs
(order 2)
10 pairs
(order 3)
16 pairs
(order 4)
|

|
'piecewise linear'
|
Use this transformation when parts of the image appear distorted differently.
|
4 pairs
|
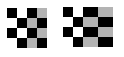
|
'lwm'
|
Use this transformation (local weighted mean), when the distortion varies locally and piecewise linear is not sufficient.
|
6 pairs
(12 pairs recommended)
|
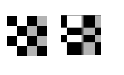
|
 | Example: Registering to a Digital Orthophoto | | Selecting Control Points |  |
© 1994-2005 The MathWorks, Inc.





