strel (Image Processing Toolbox User's Guide)

Image Processing Toolbox User's Guide

Create morphological structuring element

Syntax

```
SE = strel(shape,parameters)
```

Description

SE = strel(shape,parameters) creates a structuring element, SE, of the type specified by shape. This table lists all the supported shapes. Depending on shape, strel can take additional parameters. See the syntax descriptions that follow for details about creating each type of structuring element.

Flat Structuring Elements

'arbitrary'
'pair'

'diamond'
'periodicline'

'disk'
'rectangle'

'line'
'square'

'octagon'

Flat Structuring Elements
'arbitrary'	'pair'
'diamond'	'periodicline'
'disk'	'rectangle'
'line'	'square'
'octagon'

Nonflat Structuring Elements

'arbitrary'
'ball'

Nonflat Structuring Elements
'arbitrary'	'ball'

SE = strel('arbitrary',NHOOD) creates a flat structuring element where NHOOD specifies the neighborhood. NHOOD is a matrix containing 1's and 0's; the location of the 1's defines the neighborhood for the morphological operation. The center (or origin) of NHOOD is its center element, given by floor((size(NHOOD)+1)/2). You can omit the 'arbitrary' string and just use strel(NHOOD).

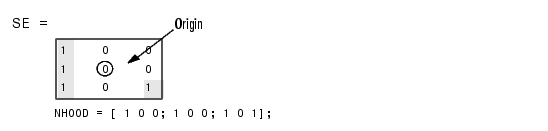
SE = strel('arbitrary',NHOOD,HEIGHT) creates a nonflat structuring element, where NHOOD specifies the neighborhood. HEIGHT is a matrix the same size as NHOOD containing the height values associated with each nonzero element of NHOOD. The HEIGHT matrix must be real and finite valued. You can omit the 'arbitrary' string and just use strel(NHOOD,HEIGHT).

SE = strel('ball',R,H,N) creates a nonflat, ball-shaped structuring element (actually an ellipsoid) whose radius in the X-Y plane is R and whose height is H. Note that R must be a nonnegative integer, H must be a real scalar, and N must be an even nonnegative integer. When N is greater than 0, the ball-shaped structuring element is approximated by a sequence of N nonflat, line-shaped structuring elements. When N equals 0, no approximation is used, and the structuring element members consist of all pixels whose centers are no greater than R away from the origin. The corresponding height values are determined from the formula of the ellipsoid specified by R and H. If N is not specified, the default value is 8.

Note Morphological operations run much faster when the structuring element uses approximations (N > 0) than when it does not (N = 0).

SE = strel('diamond',R) creates a flat, diamond-shaped structuring element, where R specifies the distance from the structuring element origin to the points of the diamond. R must be a nonnegative integer scalar.

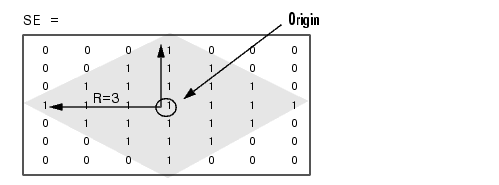
SE = strel('disk',R,N) creates a flat, disk-shaped structuring element, where R specifies the radius. R must be a nonnegative integer. N must be 0, 4, 6, or 8. When N is greater than 0, the disk-shaped structuring element is approximated by a sequence of N periodic-line structuring elements. When N equals 0, no approximation is used, and the structuring element members consist of all pixels whose centers are no greater than R away from the origin. If N is not specified, the default value is 4.

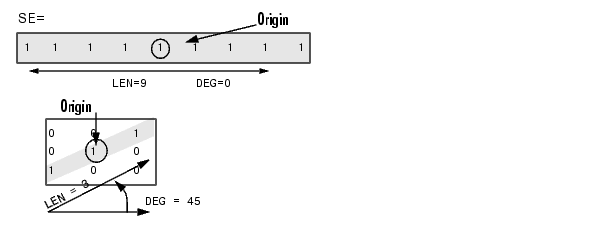
Note Morphological operations run much faster when the structuring element uses approximations (N > 0) than when it does not (N = 0). However, structuring elements that do not use approximations (N = 0) are not suitable for computing granulometries. Sometimes it is necessary for strel to use two extra line structuring elements in the approximation, in which case the number of decomposed structuring elements used is N + 2.

SE = strel('line',LEN,DEG) creates a flat, linear structuring element, where LEN specifies the length, and DEG specifies the angle (in degrees) of the line, as measured in a counterclockwise direction from the horizontal axis. LEN is approximately the distance between the centers of the structuring element members at opposite ends of the line.

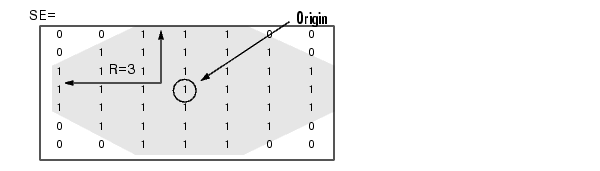
SE = strel('octagon',R) creates a flat, octagonal structuring element, where R specifies the distance from the structuring element origin to the sides of the octagon, as measured along the horizontal and vertical axes. R must be a nonnegative multiple of 3.

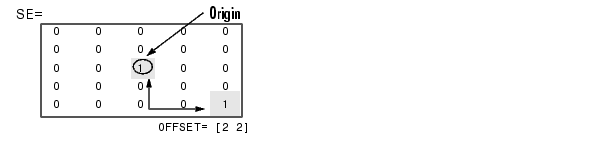
SE = strel('pair',OFFSET) creates a flat structuring element containing two members. One member is located at the origin. The second member's location is specified by the vector OFFSET. OFFSET must be a two-element vector of integers.

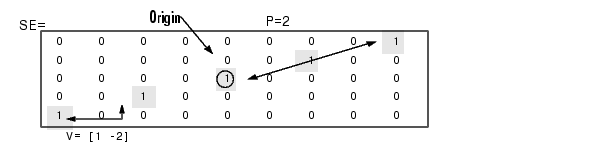
SE = strel('periodicline',P,V) creates a flat structuring element containing 2*P+1 members. V is a two-element vector containing integer-valued row and column offsets. One structuring element member is located at the origin. The other members are located at 1*V, -1*V, 2*V, -2*V, ..., P*V, -P*V.

SE = strel('rectangle',MN) creates a flat, rectangle-shaped structuring element, where MN specifies the size. MN must be a two-element vector of nonnegative integers. The first element of MN is the number of rows in the structuring element neighborhood; the second element is the number of columns.

SE = strel('square',W) creates a square structuring element whose width is W pixels. W must be a nonnegative integer scalar.

Notes

For all shapes except 'arbitrary', structuring elements are constructed using a family of techniques known collectively as structuring element decomposition. The principle is that dilation by some large structuring elements can be computed faster by dilation with a sequence of smaller structuring elements. For example, dilation by an 11-by-11 square structuring element can be accomplished by dilating first with a 1-by-11 structuring element and then with an 11-by-1 structuring element. This results in a theoretical performance improvement of a factor of 5.5, although in practice the actual performance improvement is somewhat less. Structuring element decompositions used for the 'disk' and 'ball' shapes are approximations; all other decompositions are exact.

Methods

This table lists the methods supported by the STREL object.

Method
Description

getheight
Get height of structuring element

getneighbors
Get structuring element neighbor locations and heights

getnhood
Get structuring element neighborhood

getsequence
Extract sequence of decomposed structuring elements

isflat
Return true for flat structuring element

reflect
Reflect structuring element

translate
Translate structuring element

Method	Description
`getheight`	Get height of structuring element
`getneighbors`	Get structuring element neighbor locations and heights
`getnhood`	Get structuring element neighborhood
`getsequence`	Extract sequence of decomposed structuring elements
`isflat`	Return true for flat structuring element
`reflect`	Reflect structuring element
`translate`	Translate structuring element

Example

se1 = strel('square',11)      % 11-by-11 square
se2 = strel('line',10,45)     % line, length 10, angle 45 degrees
se3 = strel('disk',15)        % disk, radius 15
se4 = strel('ball',15,5)      % ball, radius 15, height 5

Algorithm

The method used to decompose diamond-shaped structuring elements is known as "logarithmic decomposition" [1].

The method used to decompose disk structuring elements is based on the technique called "radial decomposition using periodic lines" [2], [3]. For details, see the MakeDiskStrel subfunction in toolbox/images/images/@strel/strel.m.

The method used to decompose ball structuring elements is the technique called "radial decomposition of sphere" [2].

See Also

imdilate, imerode

References

[1] van den Boomgard, Rein, and Richard van Balen, "Methods for Fast Morphological Image Transforms Using Bitmapped Images," Computer Vision, Graphics, and Image Processing: Graphical Models and Image Processing, Vol. 54, No. 3, May 1992, pp. 252-254.

[2] Adams, Rolf, "Radial Decomposition of Discs and Spheres," Computer Vision, Graphics, and Image Processing: Graphical Models and Image Processing, Vol. 55, No. 5, September 1993, pp. 325-332.

[3] Jones, Ronald, and Pierre Soille, "Periodic lines: Definition, cascades, and application to granulometrie," Pattern Recognition Letters, Vol. 17, 1996, pp. 1057-1063.

stdfilt stretchlim