Image Processing Toolbox User's Guide

Discrete Fourier Transform

Working with the Fourier transform on a computer usually involves a form of the transform known as the discrete Fourier transform (DFT). A discrete transform is a transform whose input and output values are discrete samples, making it convenient for computer manipulation. There are two principal reasons for using this form of the transform:

• The input and output of the DFT are both discrete, which makes it convenient for computer manipulations.
• There is a fast algorithm for computing the DFT known as the fast Fourier transform (FFT).

The DFT is usually defined for a discrete function 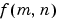that is nonzero only over the finite region 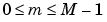and 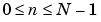. The two-dimensional M-by-N DFT and inverse M-by-N DFT relationships are given by

The values 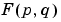are the DFT coefficients of 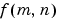. The zero-frequency coefficient, 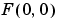, is often called the "DC component." DC is an electrical engineering term that stands for direct current. (Note that matrix indices in MATLAB always start at 1 rather than 0; therefore, the matrix elements f(1,1) and F(1,1) correspond to the mathematical quantities 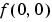and 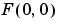, respectively.)

The MATLAB functions fft, fft2, and fftn implement the fast Fourier transform algorithm for computing the one-dimensional DFT, two-dimensional DFT, and N-dimensional DFT, respectively. The functions ifft, ifft2, and ifftn compute the inverse DFT.

Relationship to the Fourier Transform

The DFT coefficients 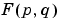are samples of the Fourier transform .

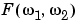Example

1. Construct a matrix f that is similar to the function f(m,n) in the example in Definition of Fourier Transform. Remember that f(m,n) is equal to 1 within the rectangular region and 0 elsewhere. Use a binary image to represent f(m,n).

• f = zeros(30,30);
  f(5:24,13:17) = 1;
  imshow(f,'notruesize')
  
  
  

2. Compute and visualize the 30-by-30 DFT of f with these commands.

• F = fft2(f);
  F2 = log(abs(F));
  imshow(F2,[-1 5],'notruesize'); colormap(jet); colorbar
  
  
  

Discrete Fourier Transform Computed Without Padding

1. This plot differs from the Fourier transform displayed in Visualizing the Fourier Transform. First, the sampling of the Fourier transform is much coarser. Second, the zero-frequency coefficient is displayed in the upper left corner instead of the traditional location in the center.

3. To obtain a finer sampling of the Fourier transform, add zero padding to f when computing its DFT. The zero padding and DFT computation can be performed in a single step with this command.

• F = fft2(f,256,256);
  

1. This command zero-pads f to be 256-by-256 before computing the DFT.

   • imshow(log(abs(F)),[-1 5]); colormap(jet); colorbar
     
     
     

Discrete Fourier Transform Computed with Padding

4. The zero-frequency coefficient, however, is still displayed in the upper left corner rather than the center. You can fix this problem by using the function fftshift, which swaps the quadrants of F so that the zero-frequency coefficient is in the center.

• F = fft2(f,256,256);
  F2 = fftshift(F);
  imshow(log(abs(F2)),[-1 5]); colormap(jet); colorbar
  

1. The resulting plot is identical to the one shown in Visualizing the Fourier Transform.

Fourier Transform

Applications of the Fourier Transform

© 1994-2005 The MathWorks, Inc.