| Image Processing Toolbox User's Guide | |
Fourier Transform
The Fourier transform is a representation of an image as a sum of complex exponentials of varying magnitudes, frequencies, and phases. The Fourier transform plays a critical role in a broad range of image processing applications, including enhancement, analysis, restoration, and compression.
This section includes the following subsections:
Definition of Fourier Transform
If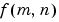 
is a function of two discrete spatial variables m and n, then the two-dimensional Fourier transform of 
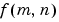is defined by the relationship
The variables 
1 and 2 are frequency variables; their units are radians per sample.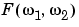 
is often called the frequency-domain representation of 
. 
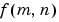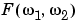is a complex-valued function that is periodic both in 
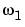and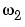 
, with period 
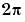. Because of the periodicity, usually only the range 
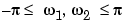is displayed. Note that 
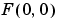is the sum of all the values of 
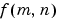. For this reason, 
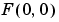is often called the constant component or DC component of the Fourier transform. (DC stands for direct current; it is an electrical engineering term that refers to a constant-voltage power source, as opposed to a power source whose voltage varies sinusoidally.)
The inverse of a transform is an operation that when performed on a transformed image produces the original image. The inverse two-dimensional Fourier transform is given by
Roughly speaking, this equation means that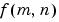 
can be represented as a sum of an infinite number of complex exponentials (sinusoids) with different frequencies. The magnitude and phase of the contribution at the frequencies 
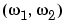are given by 
.
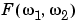Visualizing the Fourier Transform
To illustrate, consider a function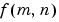 
that equals 1 within a rectangular region and 0 everywhere else. To simplify the diagram, 
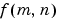is shown as a continuous function, even though the variables m and n are discrete.
The following figure shows, as a mesh plot, the magnitude of the Fourier transform,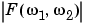 
, of the rectangular function shown in the preceding figure. The mesh plot of the magnitude is a common way to visualize the Fourier transform.
Magnitude Image of a Rectangular Function
The peak at the center of the plot is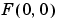 
, which is the sum of all the values in 
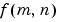. The plot also shows that 
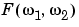has more energy at high horizontal frequencies than at high vertical frequencies. This reflects the fact that horizontal cross sections of 
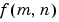are narrow pulses, while vertical cross sections are broad pulses. Narrow pulses have more high-frequency content than broad pulses.
Another common way to visualize the Fourier transform is to display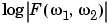 
as an image, as shown.
Log of the Fourier Transform of a Rectangular Function
Using the logarithm helps to bring out details of the Fourier transform in regions where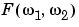 
is very close to 0.
Examples of the Fourier transform for other simple shapes are shown below.
Fourier Transforms of Some Simple Shapes
| | Transforms | Discrete Fourier Transform | |
© 1994-2005 The MathWorks, Inc.
