Quasi-Newton Algorithms :: Backpropagation (Neural Network Toolbox)

Neural Network Toolbox

Quasi-Newton Algorithms

BFGS Algorithm (trainbgf)

Newton's method is an alternative to the conjugate gradient methods for fast optimization. The basic step of Newton's method is

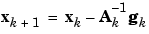
where 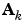is the Hessian matrix (second derivatives) of the performance index at the current values of the weights and biases. Newton's method often converges faster than conjugate gradient methods. Unfortunately, it is complex and expensive to compute the Hessian matrix for feedforward neural networks. There is a class of algorithms that is based on Newton's method, but which doesn't require calculation of second derivatives. These are called quasi-Newton (or secant) methods. They update an approximate Hessian matrix at each iteration of the algorithm. The update is computed as a function of the gradient. The quasi-Newton method that has been most successful in published studies is the Broyden, Fletcher, Goldfarb, and Shanno (BFGS) update. This algorithm has been implemented in the trainbfg routine.

In the following code, we reinitialize our previous network and retrain it using the BFGS quasi-Newton algorithm. The training parameters for trainbfg are the same as those for traincgf. The default line search routine srchbac is used in this example. The parameters show and epoch are set to 5 and 300, respectively.

p = [-1 -1 2 2;0 5 0 5];
t = [-1 -1 1 1];
net=newff(minmax(p),[3,1],{'tansig','purelin'},'trainbfg');
net.trainParam.show = 5;
net.trainParam.epochs = 300;
net.trainParam.goal = 1e-5;
[net,tr]=train(net,p,t);
   TRAINBFG-srchbac, Epoch 0/300, MSE 0.492231/1e-05, Gradient 
2.16307/1e-06
   TRAINBFG-srchbac, Epoch 5/300, MSE 0.000744953/1e-05, Gradient 
0.0196826/1e-06
   TRAINBFG-srchbac, Epoch 8/300, MSE 7.69867e-06/1e-05, Gradient 
0.00497404/1e-06
   TRAINBFG, Performance goal met.
a = sim(net,p)
a =
   -0.9995   -1.0004    1.0008    0.9945

The BFGS algorithm is described in [DeSc83]. This algorithm requires more computation in each iteration and more storage than the conjugate gradient methods, although it generally converges in fewer iterations. The approximate Hessian must be stored, and its dimension is 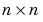, where n is equal to the number of weights and biases in the network. For very large networks it may be better to use Rprop or one of the conjugate gradient algorithms. For smaller networks, however, trainbfg can be an efficient training function.

One Step Secant Algorithm (trainoss)

Since the BFGS algorithm requires more storage and computation in each iteration than the conjugate gradient algorithms, there is need for a secant approximation with smaller storage and computation requirements. The one step secant (OSS) method is an attempt to bridge the gap between the conjugate gradient algorithms and the quasi-Newton (secant) algorithms. This algorithm does not store the complete Hessian matrix; it assumes that at each iteration, the previous Hessian was the identity matrix. This has the additional advantage that the new search direction can be calculated without computing a matrix inverse.

In the following code, we reinitialize our previous network and retrain it using the one-step secant algorithm. The training parameters for trainoss are the same as those for traincgf. The default line search routine srchbac is used in this example. The parameters show and epoch are set to 5 and 300, respectively.

p = [-1 -1 2 2;0 5 0 5];
t = [-1 -1 1 1];
net=newff(minmax(p),[3,1],{'tansig','purelin'},'trainoss');
net.trainParam.show = 5;
net.trainParam.epochs = 300;
net.trainParam.goal = 1e-5;
[net,tr]=train(net,p,t);
   TRAINOSS-srchbac, Epoch 0/300, MSE 0.665136/1e-05, Gradient 
1.61966/1e-06
   TRAINOSS-srchbac, Epoch 5/300, MSE 0.000321921/1e-05, Gradient 
0.0261425/1e-06
   TRAINOSS-srchbac, Epoch 7/300, MSE 7.85697e-06/1e-05, Gradient 
0.00527342/1e-06
   TRAINOSS, Performance goal met.
a = sim(net,p)
a =
   -1.0035   -0.9958    1.0014    0.9997

The one step secant method is described in [Batt92]. This algorithm requires less storage and computation per epoch than the BFGS algorithm. It requires slightly more storage and computation per epoch than the conjugate gradient algorithms. It can be considered a compromise between full quasi-Newton algorithms and conjugate gradient algorithms.

Line Search Routines Levenberg-Marquardt (trainlm)