Neural Network Toolbox

Levenberg-Marquardt (trainlm)

Like the quasi-Newton methods, the Levenberg-Marquardt algorithm was designed to approach second-order training speed without having to compute the Hessian matrix. When the performance function has the form of a sum of squares (as is typical in training feedforward networks), then the Hessian matrix can be approximated as

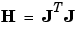
and the gradient can be computed as

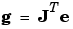
where 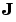is the Jacobian matrix that contains first derivatives of the network errors with respect to the weights and biases, and e is a vector of network errors. The Jacobian matrix can be computed through a standard backpropagation technique (see [HaMe94]) that is much less complex than computing the Hessian matrix.

The Levenberg-Marquardt algorithm uses this approximation to the Hessian matrix in the following Newton-like update:

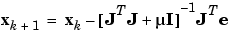
When the scalar µ is zero, this is just Newton's method, using the approximate Hessian matrix. When µ is large, this becomes gradient descent with a small step size. Newton's method is faster and more accurate near an error minimum, so the aim is to shift towards Newton's method as quickly as possible. Thus, µ is decreased after each successful step (reduction in performance function) and is increased only when a tentative step would increase the performance function. In this way, the performance function will always be reduced at each iteration of the algorithm.

In the following code, we reinitialize our previous network and retrain it using the Levenberg-Marquardt algorithm. The training parameters for trainlm are epochs, show, goal, time, min_grad, max_fail, mu, mu_dec, mu_inc, mu_max, mem_reduc. We have discussed the first six parameters earlier. The parameter mu is the initial value for µ. This value is multiplied by mu_dec whenever the performance function is reduced by a step. It is multiplied by mu_inc whenever a step would increase the performance function. If mu becomes larger than mu_max, the algorithm is stopped. The parameter mem_reduc is used to control the amount of memory used by the algorithm. It is discussed in the next section. The parameters show and epoch are set to 5 and 300, respectively.

• p = [-1 -1 2 2;0 5 0 5];
  t = [-1 -1 1 1];
  net=newff(minmax(p),[3,1],{'tansig','purelin'},'trainlm');
  net.trainParam.show = 5;
  net.trainParam.epochs = 300;
  net.trainParam.goal = 1e-5;
  [net,tr]=train(net,p,t);
     TRAINLM, Epoch 0/300, MSE 2.7808/1e-05, Gradient 7.77931/1e-10
     TRAINLM, Epoch 4/300, MSE 3.67935e-08/1e-05, Gradient 
  0.000808272/1e-10
     TRAINLM, Performance goal met.
  a = sim(net,p)
  a =
     -1.0000   -1.0000    1.0000    0.9996
  

The original description of the Levenberg-Marquardt algorithm is given in [Marq63]. The application of Levenberg-Marquardt to neural network training is described in [HaMe94] and starting on page 12-19 of [HDB96]. This algorithm appears to be the fastest method for training moderate-sized feedforward neural networks (up to several hundred weights). It also has a very efficient MATLAB® implementation, since the solution of the matrix equation is a built-in function, so its attributes become even more pronounced in a MATLAB setting.

Try the Neural Network Design Demonstration nnd12m [HDB96] for an illustration of the performance of the batch Levenberg-Marquardt algorithm.

Quasi-Newton Algorithms

Reduced Memory Levenberg-Marquardt (trainlm)

© 1994-2005 The MathWorks, Inc.