Reduced Memory Levenberg-Marquardt (trainlm) :: Backpropagation (Neural Network Toolbox)

Neural Network Toolbox

Reduced Memory Levenberg-Marquardt (trainlm)

The main drawback of the Levenberg-Marquardt algorithm is that it requires the storage of some matrices that can be quite large for certain problems. The size of the Jacobian matrix is 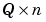, where Q is the number of training sets and n is the number of weights and biases in the network. It turns out that this matrix does not have to be computed and stored as a whole. For example, if we were to divide the Jacobian into two equal submatrices we could compute the approximate Hessian matrix as follows:

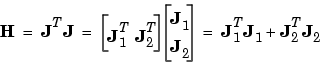
Therefore, the full Jacobian does not have to exist at one time. The approximate Hessian can be computed by summing a series of subterms. Once one subterm has been computed, the corresponding submatrix of the Jacobian can be cleared.

When using the training function trainlm, the parameter mem_reduc is used to determine how many rows of the Jacobian are to be computed in each submatrix. If mem_reduc is set to 1, then the full Jacobian is computed, and no memory reduction is achieved. If mem_reduc is set to 2, then only half of the Jacobian will be computed at one time. This saves half of the memory used by the calculation of the full Jacobian.

There is a drawback to using memory reduction. A significant computational overhead is associated with computing the Jacobian in submatrices. If you have enough memory available, then it is better to set mem_reduc to 1 and to compute the full Jacobian. If you have a large training set, and you are running out of memory, then you should set mem_reduc to 2, and try again. If you still run out of memory, continue to increase mem_reduc.

Even if you use memory reduction, the Levenberg-Marquardt algorithm will always compute the approximate Hessian matrix, which has dimensions 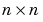. If your network is very large, then you may run out of memory. If this is the case, then you will want to try trainscg, trainrp, or one of the conjugate gradient algorithms.

Levenberg-Marquardt (trainlm) Speed and Memory Comparison