

| Neural Network Toolbox |   |
LMS Algorithm (learnwh)
The LMS algorithm, or Widrow-Hoff learning algorithm, is based on an approximate steepest descent procedure. Here again, linear networks are trained on examples of correct behavior.
Widrow and Hoff had the insight that they could estimate the mean square error by using the squared error at each iteration. If we take the partial derivative of the squared error with respect to the weights and biases at the kth iteration we have
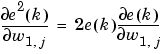
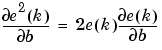
Next look at the partial derivative with respect to the error.
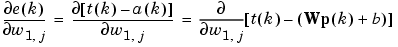 or
or
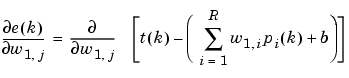
Here pi(k) is the ith element of the input vector at the kth iteration.
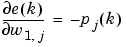
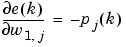 and
and
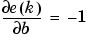
Finally, the change to the weight matrix and the bias will be
These two equations form the basis of the Widrow-Hoff (LMS) learning algorithm.
These results can be extended to the case of multiple neurons, and written in matrix form as
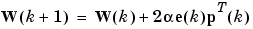
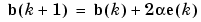
Here the error e and the bias b are vectors and 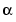 is a learning rate. If
is a learning rate. If 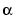 is large, learning occurs quickly, but if it is too large it may lead to instability and errors may even increase. To ensure stable learning, the learning rate must be less than the reciprocal of the largest eigenvalue of the correlation matrix
is large, learning occurs quickly, but if it is too large it may lead to instability and errors may even increase. To ensure stable learning, the learning rate must be less than the reciprocal of the largest eigenvalue of the correlation matrix 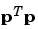 of the input vectors.
of the input vectors.
You might want to read some of Chapter 10 of [HDB96] for more information about the LMS algorithm and its convergence.
Fortunately we have a toolbox function learnwh that does all of the calculation for us. It calculates the change in weights as
The constant 2, shown a few lines above, has been absorbed into the code learning rate lr. The function maxlinlr calculates this maximum stable learning rate lr as 0.999 * P'*P.
Type help learnwh and help maxlinlr for more details about these two functions.
 | Linear Filter | Linear Classification (train) |  |
© 1994-2005 The MathWorks, Inc.