Neural Network Toolbox

Linear Classification (train)

Linear networks can be trained to perform linear classification with the function train. This function applies each vector of a set of input vectors and calculates the network weight and bias increments due to each of the inputs according to learnp. Then the network is adjusted with the sum of all these corrections. We will call each pass through the input vectors an epoch. This contrasts with adapt, discussed in Adaptive Filters and Adaptive Training, which adjusts weights for each input vector as it is presented.

Finally, train applies the inputs to the new network, calculates the outputs, compares them to the associated targets, and calculates a mean square error. If the error goal is met, or if the maximum number of epochs is reached, the training is stopped and train returns the new network and a training record. Otherwise train goes through another epoch. Fortunately, the LMS algorithm converges when this procedure is executed.

To illustrate this procedure, we will work through a simple problem. Consider the linear network introduced earlier in this chapter.

Next suppose we have the classification problem presented in Linear Filters.

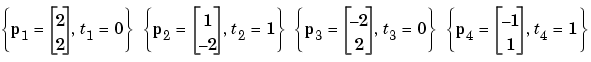
Here we have four input vectors, and we would like a network that produces the output corresponding to each input vector when that vector is presented.

We will use train to get the weights and biases for a network that produces the correct targets for each input vector. The initial weights and bias for the new network will be 0 by default. We will set the error goal to 0.1 rather than accept its default of 0.

• P = [2 1 -2 -1;2 -2 2 1];
  t = [0 1 0 1];
  net = newlin( [-2 2; -2 2],1);
  net.trainParam.goal= 0.1;
  [net, tr] = train(net,P,t); 
  

The problem runs, producing the following training record.

• TRAINB, Epoch 0/100, MSE 0.5/0.1.
  TRAINB, Epoch 25/100, MSE 0.181122/0.1.
  TRAINB, Epoch 50/100, MSE 0.111233/0.1.
  TRAINB, Epoch 64/100, MSE 0.0999066/0.1.
  TRAINB, Performance goal met.
  

Thus, the performance goal is met in 64 epochs. The new weights and bias are

• weights = net.iw{1,1}
  weights =
     -0.0615   -0.2194
  bias = net.b(1)
  bias =
      [0.5899]
  

We can simulate the new network as shown below.

• A = sim(net, p)
  A =
      0.0282    0.9672    0.2741    0.4320,
  

We also can calculate the error.

• err = t - sim(net,P)
  err =
     -0.0282    0.0328   -0.2741    0.5680
  

Note that the targets are not realized exactly. The problem would have run longer in an attempt to get perfect results had we chosen a smaller error goal, but in this problem it is not possible to obtain a goal of 0. The network is limited in its capability. See Limitations and Cautions at the end of this chapter for examples of various limitations.

This demonstration program demolin2 shows the training of a linear neuron, and plots the weight trajectory and error during training.

You also might try running the demonstration program nnd10lc. It addresses a classic and historically interesting problem, shows how a network can be trained to classify various patterns, and how the trained network responds when noisy patterns are presented.

LMS Algorithm (learnwh)

Limitations and Cautions

© 1994-2005 The MathWorks, Inc.