Limitations and Cautions :: Linear Filters (Neural Network Toolbox)

Neural Network Toolbox

Limitations and Cautions

Linear networks may only learn linear relationships between input and output vectors. Thus, they cannot find solutions to some problems. However, even if a perfect solution does not exist, the linear network will minimize the sum of squared errors if the learning rate lr is sufficiently small. The network will find as close a solution as is possible given the linear nature of the network's architecture. This property holds because the error surface of a linear network is a multidimensional parabola. Since parabolas have only one minimum, a gradient descent algorithm (such as the LMS rule) must produce a solution at that minimum.

Linear networks have other various limitations. Some of them are discussed below.

Overdetermined Systems

Consider an overdetermined system. Suppose that we have a network to be trained with four 1-element input vectors and four targets. A perfect solution to 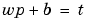for each of the inputs may not exist, for there are four constraining equations and only one weight and one bias to adjust. However, the LMS rule will still minimize the error. You might try demolin4 to see how this is done.

Underdetermined Systems

Consider a single linear neuron with one input. This time, in demolin5, we will train it on only one one-element input vector and its one-element target vector:

```
P = [+1.0];
T = [+0.5];
```

Note that while there is only one constraint arising from the single input/target pair, there are two variables, the weight and the bias. Having more variables than constraints results in an underdetermined problem with an infinite number of solutions. You can try demoin5 to explore this topic.

Linearly Dependent Vectors

Normally it is a straightforward job to determine whether or not a linear network can solve a problem. Commonly, if a linear network has at least as many degrees of freedom (S*R+S = number of weights and biases) as constraints (Q = pairs of input/target vectors), then the network can solve the problem. This is true except when the input vectors are linearly dependent and they are applied to a network without biases. In this case, as shown with demonstration script demolin6, the network cannot solve the problem with zero error. You might want to try demolin6.

Too Large a Learning Rate

A linear network can always be trained with the Widrow-Hoff rule to find the minimum error solution for its weights and biases, as long as the learning rate is small enough. Demonstration script demolin7 shows what happens when a neuron with one input and a bias is trained with a learning rate larger than that recommended by maxlinlr. The network is trained with two different learning rates to show the results of using too large a learning rate.

Linear Classification (train) Summary