Neural Network Toolbox

Outliers and the Normalized Perceptron Rule

Long training times can be caused by the presence of an outlier input vector whose length is much larger or smaller than the other input vectors. Applying the perceptron learning rule involves adding and subtracting input vectors from the current weights and biases in response to error. Thus, an input vector with large elements can lead to changes in the weights and biases that take a long time for a much smaller input vector to overcome. You might want to try demop4 to see how an outlier affects the training.

By changing the perceptron learning rule slightly, training times can be made insensitive to extremely large or small outlier input vectors.

Here is the original rule for updating weights:

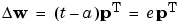
As shown above, the larger an input vector p, the larger its effect on the weight vector w. Thus, if an input vector is much larger than other input vectors, the smaller input vectors must be presented many times to have an effect.

The solution is to normalize the rule so that effect of each input vector on the weights is of the same magnitude:

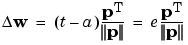
The normalized perceptron rule is implemented with the function learnpn, which is called exactly like learnpn. The normalized perceptron rule function learnpn takes slightly more time to execute, but reduces the number of epochs considerably if there are outlier input vectors. You might try demop5 to see how this normalized training rule works.

Limitations and Cautions

Graphical User Interface

© 1994-2005 The MathWorks, Inc.