

| Neural Network Toolbox |   |
Perceptron Learning Rule (learnp)
Perceptrons are trained on examples of desired behavior. The desired behavior can be summarized by a set of input, output pairs
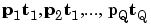
where p is an input to the network and t is the corresponding correct (target) output. The objective is to reduce the error e, which is the difference 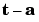 between the neuron response a, and the target vector t. The perceptron learning rule
between the neuron response a, and the target vector t. The perceptron learning rule learnp calculates desired changes to the perceptron's weights and biases given an input vector p, and the associated error e. The target vector t must contain values of either 0 or 1, as perceptrons (with hardlim transfer functions) can only output such values.
Each time learnp is executed, the perceptron has a better chance of producing the correct outputs. The perceptron rule is proven to converge on a solution in a finite number of iterations if a solution exists.
If a bias is not used, learnp works to find a solution by altering only the weight vector w to point toward input vectors to be classified as 1, and away from vectors to be classified as 0. This results in a decision boundary that is perpendicular to w, and which properly classifies the input vectors.
There are three conditions that can occur for a single neuron once an input vector p is presented and the network's response a is calculated:
CASE 1.. If an input vector is presented and the output of the neuron is correct (a = t, and e = t - a = 0), then the weight vector w is not altered.
CASE 2. . If the neuron output is 0 and should have been 1 (a = 0 and t = 1, and e = t - a = 1), the input vector p is added to the weight vector w. This makes the weight vector point closer to the input vector, increasing the chance that the input vector will be classified as a 1 in the future.
CASE 3.. If the neuron output is 1 and should have been 0 (a = 1 and t = 0, and e = t - a = -1), the input vector p is subtracted from the weight vector w. This makes the weight vector point farther away from the input vector, increasing the chance that the input vector is classified as a 0 in the future.
The perceptron learning rule can be written more succinctly in terms of the error e = t - a, and the change to be made to the weight vector 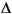 w:
w:
CASE 1.. If e = 0, then make a change 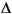 w equal to 0.
w equal to 0.
CASE 2. . If e = 1, then make a change 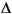 w equal to pT.
w equal to pT.
CASE 3. . If e = -1, then make a change 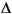 w equal to -pT.
w equal to -pT.
All three cases can then be written with a single expression:
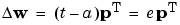
We can get the expression for changes in a neuron's bias by noting that the bias is simply a weight that always has an input of 1:
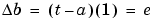
For the case of a layer of neurons we have:
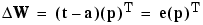 and
and
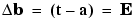
The Perceptron Learning Rule can be summarized as follows
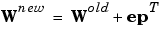 and
and
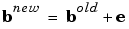
Now let us try a simple example. We start with a single neuron having an input vector with just two elements.
To simplify matters we set the bias equal to 0 and the weights to 1 and -0.8.
The input target pair is given by
We can compute the output and error with
and finally use the function learnp to find the change in the weights.
The new weights, then, are obtained as
The process of finding new weights (and biases) can be repeated until there are no errors. Note that the perceptron learning rule is guaranteed to converge in a finite number of steps for all problems that can be solved by a perceptron. These include all classification problems that are "linearly separable." The objects to be classified in such cases can be separated by a single line.
You might want to try demo nnd4pr. It allows you to pick new input vectors and apply the learning rule to classify them.
 | Learning Rules | Training (train) |  |
© 1994-2005 The MathWorks, Inc.