Training (train) :: Perceptrons (Neural Network Toolbox)

Neural Network Toolbox

Training (train)

If sim and learnp are used repeatedly to present inputs to a perceptron, and to change the perceptron weights and biases according to the error, the perceptron will eventually find weight and bias values that solve the problem, given that the perceptron can solve it. Each traverse through all of the training input and target vectors is called a pass.

The function train carries out such a loop of calculation. In each pass the function train proceeds through the specified sequence of inputs, calculating the output, error and network adjustment for each input vector in the sequence in which the inputs are presented.

Note that train does not guarantee that the resulting network does its job. The new values of W and b must be checked by computing the network output for each input vector to see if all targets are reached. If a network does not perform successfully it can be trained further by again calling train with the new weights and biases for more training passes, or the problem can be analyzed to see if it is a suitable problem for the perceptron. Problems which are not solvable by the perceptron network are discussed in the "Limitations and Cautions" section.

To illustrate the training procedure, we will work through a simple problem. Consider a one neuron perceptron with a single vector input having two elements.

This network, and the problem we are about to consider, are simple enough that you can follow through what is done with hand calculations if you want. The problem discussed below follows that found in [HDB1996].

Let us suppose we have the following classification problem and would like to solve it with our single vector input, two-element perceptron network.

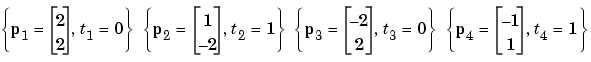
Use the initial weights and bias. We denote the variables at each step of this calculation by using a number in parentheses after the variable. Thus, above, we have the initial values, W(0) and b(0).

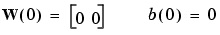
We start by calculating the perceptron's output a for the first input vector p1, using the initial weights and bias.

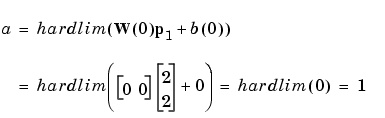
The output a does not equal the target value t₁, so we use the perceptron rule to find the incremental changes to the weights and biases based on the error.

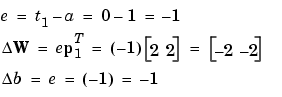
You can calculate the new weights and bias using the perceptron update rules shown previously.

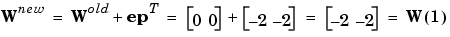
Now present the next input vector, p2. The output is calculated below.

On this occasion, the target is 1, so the error is zero. Thus there are no changes in weights or bias, so

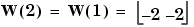and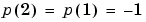

We can continue in this fashion, presenting p3 next, calculating an output and the error, and making changes in the weights and bias, etc. After making one pass through all of the four inputs, you get the values: 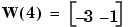and 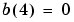. To determine if we obtained a satisfactory solution, we must make one pass through all input vectors to see if they all produce the desired target values. This is not true for the 4th input, but the algorithm does converge on the 6th presentation of an input. The final values are:

and

This concludes our hand calculation. Now, how can we do this using the train function?

The following code defines a perceptron like that shown in the previous figure, with initial weights and bias values of 0.

```
net = newp([-2 2;-2 +2],1);
```

Now consider the application of a single input.

```
p =[2; 2];
having the target
t =[0];
```

Now set epochs to 1, so that train will go through the input vectors (only one here) just one time.

net.trainParam.epochs = 1;
net = train(net,p,t);

The new weights and bias are

```
w =
    -2    -2
b =
    -1
```

Thus, the initial weights and bias are 0, and after training on only the first vector, they have the values [-2 -2] and -1, just as we hand calculated.

We now apply the second input vector 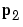. The output is 1, as it will be until the weights and bias are changed, but now the target is 1, the error will be 0 and the change will be zero. We could proceed in this way, starting from the previous result and applying a new input vector time after time. But we can do this job automatically with train.

Now let's apply train for one epoch, a single pass through the sequence of all four input vectors. Start with the network definition.

net = newp([-2 2;-2 +2],1);
net.trainParam.epochs = 1;

The input vectors and targets are

p = [[2;2] [1;-2] [-2;2] [-1;1]]
t =[0 1 0 1]

Now train the network with

```
net = train(net,p,t);
```

The new weights and bias are

```
w =
    -3    -1
b =
     0
```

Note that this is the same result as we got previously by hand. Finally simulate the trained network for each of the inputs.

a = sim(net,p)
a = 
    [0]    [0]    [1]    [1]

The outputs do not yet equal the targets, so we need to train the network for more than one pass. We will try four epochs. This run gives the following results.

TRAINC, Epoch 0/20
TRAINC, Epoch 3/20
TRAINC, Performance goal met.

Thus, the network was trained by the time the inputs were presented on the third epoch. (As we know from our hand calculation, the network converges on the presentation of the sixth input vector. This occurs in the middle of the second epoch, but it takes the third epoch to detect the network convergence.) The final weights and bias are

```
w =
    -2    -3
b =
     1
```

The simulated output and errors for the various inputs are

a =
             0          1.00             0          1.00
error = [a(1)-t(1) a(2)-t(2) a(3)-t(3) a(4)-t(4)]
error =
             0             0             0             0

Thus, we have checked that the training procedure was successful. The network converged and produces the correct target outputs for the four input vectors.

Note that the default training function for networks created with newp is trains. (You can find this by executing net.trainFcn.) This training function applies the perceptron learning rule in its pure form, in that individual input vectors are applied individually in sequence, and corrections to the weights and bias are made after each presentation of an input vector. Thus, perceptron training with train will converge in a finite number of steps unless the problem presented cannot be solved with a simple perceptron.

The function train can be used in various ways by other networks as well. Type help train to read more about this basic function.

You may want to try various demonstration programs. For instance, demop1 illustrates classification and training of a simple perceptron.

Perceptron Learning Rule (learnp) Limitations and Cautions