Radial Basis Functions :: Radial Basis Networks (Neural Network Toolbox)

Neural Network Toolbox

Radial Basis Functions

Neuron Model

Here is a radial basis network with R inputs.

Notice that the expression for the net input of a radbas neuron is different from that of neurons in previous chapters. Here the net input to the radbas transfer function is the vector distance between its weight vector w and the input vector p, multiplied by the bias b. (The 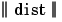box in this figure accepts the input vector p and the single row input weight matrix, and produces the dot product of the two.)

The transfer function for a radial basis neuron is:

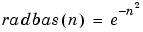
Here is a plot of the radbas transfer function.

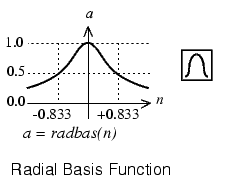
The radial basis function has a maximum of 1 when its input is 0. As the distance between w and p decreases, the output increases. Thus, a radial basis neuron acts as a detector that produces 1 whenever the input p is identical to its weight vector p.

The bias b allows the sensitivity of the radbas neuron to be adjusted. For example, if a neuron had a bias of 0.1 it would output 0.5 for any input vector p at vector distance of 8.326 (0.8326/b) from its weight vector w.

Important Radial Basis Functions Network Architecture