Network Architecture :: Radial Basis Networks (Neural Network Toolbox)

Neural Network Toolbox

Network Architecture

Radial basis networks consist of two layers: a hidden radial basis layer of S¹ neurons, and an output linear layer of S² neurons.

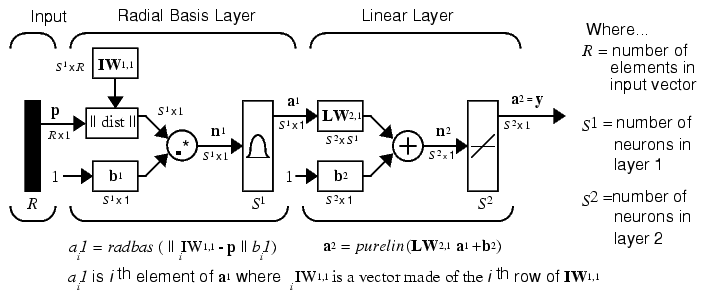
The 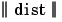box in this figure accepts the input vector p and the input weight matrix IW^1,1, and produces a vector having S₁elements. The elements are the distances between the input vector and vectors_iIW^1,1formed from the rows of the input weight matrix.

The bias vector b¹ and the output of 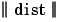are combined with the MATLAB® operation .* , which does element-by-element multiplication.

The output of the first layer for a feed forward network net can be obtained with the following code:

a{1} = radbas(netprod(dist(net.IW{1,1},p),net.b{1}))

Fortunately, you won't have to write such lines of code. All of the details of designing this network are built into design functions newrbe and newrb, and their outputs can be obtained with sim.

We can understand how this network behaves by following an input vector p through the network to the output a². If we present an input vector to such a network, each neuron in the radial basis layer will output a value according to how close the input vector is to each neuron's weight vector.

Thus, radial basis neurons with weight vectors quite different from the input vector p have outputs near zero. These small outputs have only a negligible effect on the linear output neurons.

In contrast, a radial basis neuron with a weight vector close to the input vector p produces a value near 1. If a neuron has an output of 1 its output weights in the second layer pass their values to the linear neurons in the second layer.

In fact, if only one radial basis neuron had an output of 1, and all others had outputs of 0's (or very close to 0), the output of the linear layer would be the active neuron's output weights. This would, however, be an extreme case. Typically several neurons are always firing, to varying degrees.

Now let us look in detail at how the first layer operates. Each neuron's weighted input is the distance between the input vector and its weight vector, calculated with dist. Each neuron's net input is the element-by-element product of its weighted input with its bias, calculated with netprod. Each neuron's output is its net input passed through radbas. If a neuron's weight vector is equal to the input vector (transposed), its weighted input is 0, its net input is 0, and its output is 1. If a neuron's weight vector is a distance of spread from the input vector, its weighted input is spread, its net input is sqrt(-log(.5)) (or 0.8326), therefore its output is 0.5.

Radial Basis Functions Exact Design (newrbe)