bilinear (Signal Processing Toolbox)

Bilinear transformation method for analog-to-digital filter conversion

Syntax

[zd,pd,kd] = bilinear(z,p,k,fs)
[zd,pd,kd] = bilinear(z,p,k,fs,fp)
[numd,dend] = bilinear(num,den,fs)
[numd,dend] = bilinear(num,den,fs,fp)
[Ad,Bd,Cd,Dd] = bilinear(A,B,C,D,fs)
[Ad,Bd,Cd,Dd] = bilinear(A,B,C,D,fs,fp)

Description

The bilinear transformation is a mathematical mapping of variables. In digital filtering, it is a standard method of mapping the s or analog plane into the z or digital plane. It transforms analog filters, designed using classical filter design techniques, into their discrete equivalents.

The bilinear transformation maps the s-plane into the z-plane by

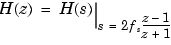
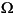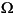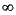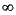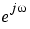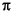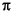This transformation maps the j axis (from = - to +) repeatedly around the unit circle (, from =- to ) by

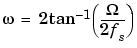
bilinear can accept an optional parameter Fp that specifies prewarping. fp, in hertz, indicates a "match" frequency, that is, a frequency for which the frequency responses before and after mapping match exactly. In prewarped mode, the bilinear transformation maps the s-plane into the z-plane with

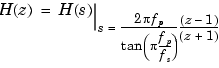
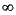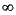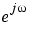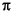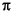With the prewarping option, bilinear maps the j axis (from = - to +) repeatedly around the unit circle (, from =- to ) by

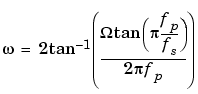
In prewarped mode, bilinear matches the frequency 2f_p (in radians per second) in the s-plane to the normalized frequency 2f_p/f_s (in radians per second) in the z-plane.

The bilinear function works with three different linear system representations: zero-pole-gain, transfer function, and state-space form.

Zero-Pole-Gain

[zd,pd,kd] = bilinear(z,p,k,fs) and

[zd,pd,kd] = bilinear(z,p,k,fs,fp) convert the s-domain transfer function specified by z, p, and k to a discrete equivalent. Inputs z and p are column vectors containing the zeros and poles, k is a scalar gain, and fs is the sampling frequency in hertz. bilinear returns the discrete equivalent in column vectors zd and pd and scalar kd. The optional match frequency, fp is in hertz and is used for prewarping.

Transfer Function

[numd,dend] = bilinear(num,den,fs) and

[numd,dend] = bilinear(num,den,fs,fp) convert an s-domain transfer function given by num and den to a discrete equivalent. Row vectors num and den specify the coefficients of the numerator and denominator, respectively, in descending powers of s.

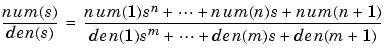
fs is the sampling frequency in hertz. bilinear returns the discrete equivalent in row vectors numd and dend in descending powers of z (ascending powers of z^-1). fp is the optional match frequency, in hertz, for prewarping.

State-Space

[Ad,Bd,Cd,Dd] = bilinear(A,B,C,D,fs) and

[Ad,Bd,Cd,Dd] = bilinear(A,B,C,D,fs,fp) convert the continuous-time state-space system in matrices A, B, C, D

to the discrete-time system:

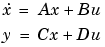
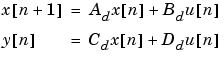
fs is the sampling frequency in hertz. bilinear returns the discrete equivalent in matrices Ad, Bd, Cd, Dd. The optional match frequency, fp is in hertz and is used for prewarping.

Algorithm

bilinear uses one of two algorithms depending on the format of the input linear system you supply. One algorithm works on the zero-pole-gain format and the other on the state-space format. For transfer function representations, bilinear converts to state-space form, performs the transformation, and converts the resulting state-space system back to transfer function form.

Zero-Pole-Gain Algorithm

For a system in zero-pole-gain form, bilinear performs four steps:

If fp is present, it prewarps:

 fp = 2*pi*fp;
 fs = fp/tan(fp/fs/2)

otherwise, fs = 2*fs.

It strips any zeros at ± using

```
 z = z(finite(z));
```

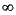It transforms the zeros, poles, and gain using

 pd = (1+p/fs)./(1-p/fs);%Do bilinear transformation
 zd = (1+z/fs)./(1-z/fs);
 kd = real(k*prod(fs-z)./prod(fs-p));

It adds extra zeros at -1 so the resulting system has equivalent numerator and denominator order.

State-Space Algorithm

For a system in state-space form, bilinear performs two steps:

If fp is present, k = 2*pi*fp/tan(pi*fp/fs); else k = 2*fs.
It computes Ad, Bd, Cd, and Dd in terms of A, B, C, and D using

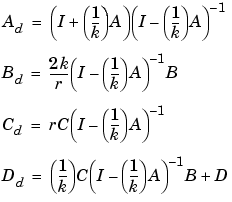
bilinear implements these relations using conventional MATLAB statements. The scalar r is arbitrary; bilinear uses 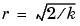to ensure good quantization noise properties in the resulting system.

Diagnostics

bilinear requires that the numerator order be no greater than the denominator order. If this is not the case, bilinear displays

Numerator cannot be higher order than denominator.

For bilinear to distinguish between the zero-pole-gain and transfer function linear system formats, the first two input parameters must be vectors with the same orientation in these cases. If this is not the case, bilinear displays

First two arguments must have the same orientation.

See Also

impinvar, lp2bp, lp2bs, lp2hp, lp2lp

References

[1] Parks, T.W., and C.S. Burrus. Digital Filter Design. New York: John Wiley & Sons, 1987. Pgs. 209-213.

[2] Oppenheim, A.V., and R.W. Schafer. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999, pp. 450-454.

besself bitrevorder