Signal Processing Toolbox

lp2lp

Change cutoff frequency for lowpass analog filter

Syntax

• [bt,at] = lp2lp(b,a,Wo)
  [At,Bt,Ct,Dt] = lp2lp(A,B,C,D,Wo)
  

Description

lp2lp transforms an analog lowpass filter prototype with a cutoff angular frequency of 1 rad/s into a lowpass filter with any specified cutoff angular frequency. The transformation is one step in the digital filter design process for the butter, cheby1, cheby2, and ellip functions.

The lp2lp function can perform the transformation on two different linear system representations: transfer function form and state-space form. In both cases, the input system must be an analog filter prototype.

Transfer Function Form (Polynomial)

[bt,at] = lp2lp(b,a,Wo) transforms an analog lowpass filter prototype given by polynomial coefficients into a lowpass filter with cutoff angular frequency Wo. Row vectors b and a specify the coefficients of the numerator and denominator of the prototype in descending powers of s.

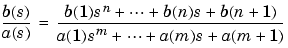
Scalar Wo specifies the cutoff angular frequency in units of radians/second. lp2lp returns the frequency transformed filter in row vectors bt and at.

State-Space Form

[At,Bt,Ct,Dt] = lp2lp(A,B,C,D,Wo) converts the continuous-time state-space lowpass filter prototype in matrices A, B, C, D below

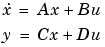
into a lowpass filter with cutoff angular frequency Wo. lp2lp returns the lowpass filter in matrices At, Bt, Ct, Dt.

Algorithm

lp2lp is a highly accurate state-space formulation of the classic analog filter frequency transformation. If a lowpass filter is to have cutoff angular frequency ₀, the standard s-domain transformation is

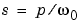
The state-space version of this transformation is

• At = Wo*A;
  Bt = Wo*B;
  Ct = C;
  Dt = D;
  

See lp2bp for a derivation of the bandpass version of this transformation.

See Also

bilinear, impinvar, lp2bp, lp2bs, lp2hp

lp2hp

lpc

© 1994-2005 The MathWorks, Inc.