chirp (Signal Processing Toolbox)

Swept-frequency cosine

Syntax

y = chirp(t,f0,t1,f1)
y = chirp(t,f0,t1,f1,'method')
y = chirp(t,f0,t1,f1,'method',phi)
y = chirp(t,f0,t1,f1,'quadratic',phi,'shape')

Description

y = chirp(t,f0,t1,f1) generates samples of a linear swept-frequency cosine signal at the time instances defined in array t, where f0 is the instantaneous frequency at time 0, and f1 is the instantaneous frequency at time t1. f0 and f1 are both in hertz. If unspecified, f0 is e^-6 for logarithmic chirp and 0 for all other methods, t1 is 1, and f1 is 100.

Y = CHIRP(T,F0,T1,F1,'method') specifies alternative sweep method options, where method can be:

linear, which specifies an instantaneous frequency sweep f_i(t) given by

where

ensures that the desired frequency breakpoint f₁ at time t₁ is maintained.

quadratic, which specifies an instantaneous frequency sweep f_i(t) given by

where

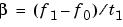
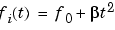
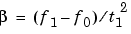
If f₀ > f₁ (downsweep), the default shape is convex. If f₀< f₁ (upsweep), the default shape is concave.

logarithmic specifies an instantaneous frequency sweep f_i(t) given by

where

Both an upsweep (f₁> f₀) and a downsweep (f₀ > f₁) of frequency is possible.

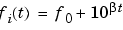
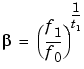
Each of the above methods can be entered as 'li', 'q', and 'lo', respectively.

y = chirp(t,f0,t1,f1,'method',phi) allows an initial phase phi to be specified in degrees. If unspecified, phi is 0. Default values are substituted for empty or omitted trailing input arguments.

y = chirp(t,f0,t1,f1,'quadratic',phi,'shape') specifies the shape of the quadratic swept-frequency signal's spectrogram. shape is either concave or convex, which describes the shape of the parabola in the positive frequency axis. If shape is omitted, the default is convex for downsweep (f₀ > f₁) and is concave for upsweep (f₀< f₁).

In the following illustration are the shapes of a convex downsweep and a concave upsweep. The convex downsweep is shaped like the profile of a portion of an inverted bowl. It sweeps from high to low frequency. The concave upsweep is shaped like the profile of a portion an upright bowl. It sweeps from low to high frequency.

Examples

Example 1

Compute the spectrogram of a chirp with linear instantaneous frequency deviation:

t = 0:0.001:2;              % 2 secs @ 1kHz sample rate
y = chirp(t,0,1,150);       % Start @ DC, cross 150Hz at t=1 sec
spectrogram(y,256,250,256,1E3,'yaxis')

Example 2

Compute the spectrogram of a chirp with quadratic instantaneous frequency deviation:

t = -2:0.001:2;                     % ±2 secs @ 1kHz sample rate
y = chirp(t,100,1,200,'quadratic'); % Start @ 100Hz, cross 200Hz 
                                    %   at t=1 sec
spectrogram(y,128,120,128,1E3,'yaxis')

Example 3

Compute the spectrogram of a convex quadratic chirp:

t = -1:0.001:1;                   % +/-1 second @ 1kHz sample rate
fo = 100; f1 = 400; % Start at 100Hz, go up to 400Hz
y = chirp(t,fo,1,f1,'q',[],'convex');
spectrogram(y,256,200,256,1000,'yaxis')

Example 4

Compute the spectrogram of a concave quadratic chirp:

t = 0:0.001:1;                    % 1 second @ 1kHz sample rate
fo = 100; f1 = 25;                % Start at 100Hz, go down to 25Hz
y = chirp(t,fo,1,f1,'q',[],'concave');
spectrogram(y,hanning(256),128,256,1000,'yaxis')

Example 5

Compute the spectrogram of a logarithmic chirp:

t = 0:0.001:10;                   % 10 seconds @ 1kHz sample rate
fo = 10; f1 = 400;                % Start at 10Hz, go up to 400Hz
y = chirp(t,fo,10,f1,'logarithmic');
spectrogram(y,256,200,256,1000,'yaxis')

See Also

cos, diric, gauspuls, pulstran, rectpuls, sawtooth, sin, sinc, square, tripuls

cheby2 conv