sinc (Signal Processing Toolbox)

Signal Processing Toolbox

sinc

Sinc function

Syntax

```
y = sinc(x)
```

Description

sinc computes the sinc function of an input vector or array, where the sinc function is

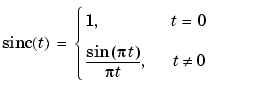
This function is the continuous inverse Fourier transform of the rectangular pulse of width 2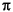 and height 1.

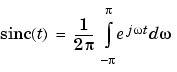
y = sinc(x) returns an array y the same size as x, whose elements are the sinc function of the elements of x.

The space of functions bandlimited in the frequency range 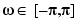is spanned by the infinite (yet countable) set of sinc functions shifted by integers. Thus any such bandlimited function g(t) can be reconstructed from its samples at integer spacings.

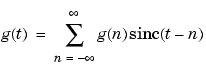
Examples

Perform ideal bandlimited interpolation by assuming that the signal to be interpolated is 0 outside of the given time interval and that it has been sampled at exactly the Nyquist frequency:

t = (1:10)';                 % A column vector of time samples
randn('state',0);
x = randn(size(t));          % A column vector of data
ts = linspace(-5,15,600)';   % times at which to interpolate data
y = sinc(ts(:,ones(size(t))) - t(:,ones(size(ts)))')*x;
plot(t,x,'o',ts,y)

See Also

chirp, cos, diric, gauspuls, pulstran, rectpuls, sawtooth, sin, square, tripuls

sigwin sos2cell