dpss (Signal Processing Toolbox)

Discrete prolate spheroidal sequences (Slepian sequences)

Syntax

[e,v] = dpss(n,nw)
[e,v] = dpss(n,nw,k)
[e,v] = dpss(n,nw,[k1 k2])
[e,v] = dpss(n,nw,'int')
[e,v] = dpss(n,nw,'int',Ni)
[e,v] = dpss(...,'trace')

Description

[e,v] = dpss(n,nw) generates the first 2*nw discrete prolate spheroidal sequences (DPSS) of length n in the columns of e, and their corresponding concentrations in vector v. They are also generated in the DPSS MAT-file database dpss.mat. nw must be less than n/2.

[e,v] = dpss(n,nw,k) returns the k most band-limited discrete prolate spheroidal sequences. k must be an integer such that 1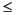k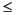n.

[e,v] = dpss(n,nw,[k1 k2]) returns the k1st through the k2nd discrete prolate spheroidal sequences, where 1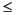k1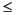k2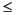n.

For all of the above forms:

The Slepian sequences are calculated directly.
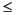
The sequences are generated in the frequency band || (2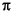W), where W = nw/n is the half-bandwidth and is in rad/sample.
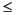
e(:,1) is the length n signal most concentrated in the frequency band || (2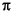W) radians, e(:,2) is the signal orthogonal to e(:,1) that is most concentrated in this band, e(:,3) is the signal orthogonal to both e(:,1) and e(:,2) that is most concentrated in this band, etc.
For multitaper spectral analysis, typical choices for nw are 2, 5/2, 3, 7/2, or 4.

[e,v] = dpss(n,nw,'int') uses the interpolation method specified by the string 'int' to compute e and v from the sequences in dpss.mat with length closest to n. The string 'int' can be either:

'spline': Use spline interpolation.
'linear': Use linear interpolation. This is much faster but less accurate than spline interpolation.

[e,v] = dpss(n,nw,'int',Ni) interpolates from existing length Ni sequences. The interpolation method 'linear' requires Ni > n.

[e,v] = dpss(...,'trace') uses the trailing string 'trace' to display which interpolation method DPSS uses. If you don't specify the interpolation method, the display indicates that you are using the direct method.

Examples

Example 1: Using dpss, dpssave, and dpssdir

Create a catalogue of 16 DPSS functions with nw = 4, and use spline interpolation on 10 of these functions while displaying the interpolation method you use. You can do this using dpss, dpsssave, and dpssdir:

% Create the catalogue of functions.
[e,v] = dpss(16,4);
% Save e and v in a MAT-file. 
dpsssave(4,e,v);
% Find nw = 4. First create a structure called index.
index = dpssdir;
index.wlists
ans = 
     NW: 4
    key: 1
% Use spline interpolation on 10 of the DPSS functions.
[e1,v1] = dpss(10,4,'spline',size(e,1),'trace');

Example 2: Using dpss and dpssload

Create a set of DPSS functions using dpss, and use the spline method on a subset of these functions. Use dpssload to load the MAT-file created by dpss:

% Create the catalogue of functions.
[e,v] = dpss(16,4);
% Load dpss.mat, where e and v are saved. 
[e1,v1] = dpssload(16,4);
% Use spline interpolation on 10 of the DPSS functions.
[e1,v1] = dpss(10,4,'spline');

See Also

dpssclear, dpssdir, dpssload, dpsssave, pmtm

References

[1] Percival, D.B., and A.T. Walden. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. Cambridge: Cambridge University Press, 1993.

downsample dpssclear