Signal Processing Toolbox

freqs

Frequency response of analog filters

Syntax

• h = freqs(b,a,w)
  [h,w] = freqs(b,a)
  [h,w] = freqs(b,a,f)
  freqs(b,a)
  

Description

freqs returns the complex frequency response H(j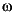) (Laplace transform) of an analog filter

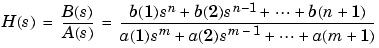
given the numerator and denominator coefficients in vectors b and a.

h = freqs(b,a,w) returns the complex frequency response of the analog filter specified by coefficient vectors b and a. freqs evaluates the frequency response along the imaginary axis in the complex plane at the angular frequencies in rad/sec specified in real vector w, which must contain more than one frequency.

[h,w] = freqs(b,a) automatically picks a set of 200 frequency points w on which to compute the frequency response h.

[h,w] = freqs(b,a,f) picks f number of frequencies on which to compute the frequency response h.

freqs with no output arguments plots the magnitude and phase response versus frequency in the current figure window.

freqs works only for real input systems and positive frequencies.

Examples

Find and graph the frequency response of the transfer function given by:

• a = [1 0.4 1];
  b = [0.2 0.3 1];
  w = logspace(-1,1);
  freqs(b,a,w)
  
  
  

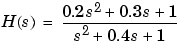
You can also create the plot with:

• h = freqs(b,a,w);
  mag = abs(h);
  phase = angle(h);
  subplot(2,1,1), loglog(w,mag)
  subplot(2,1,2), semilogx(w,phase)
  

To convert to hertz, degrees, and decibels, use:

• f = w/(2*pi);
  mag = 20*log10(mag);
  phase = phase*180/pi;
  

Algorithm

freqs evaluates the polynomials at each frequency point, then divides the numerator response by the denominator response:

• s = i*w;
  h = polyval(b,s)./polyval(a,s);
  

See Also

abs, angle, freqz, invfreqs, logspace, polyval

flattopwin

freqspace

© 1994-2005 The MathWorks, Inc.