freqz (Signal Processing Toolbox)

Frequency response of digital filters

Syntax

[h,w]= freqz(b,a,l)
h = freqz(b,a,w)
[h,w] = freqz(b,a,l,'whole')
[h,f] = freqz(b,a,l,fs)
h = freqz(b,a,f,fs)
[h,f] = freqz(b,a,l,'whole',fs)
freqz(b,a,...)
freqz(Hd)

Description

[h,w] = freqz(b,a,l) returns the frequency response vector h and the corresponding angular frequency vector w for the digital filter whose transfer function is determined by the (real or complex) numerator and denominator polynomials represented in the vectors b and a, respectively. The vectors h and w are both of length l. The angular frequency vector w has values ranging from 0 to 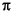radians per sample. When you don't specify the integer l, or you specify it as the empty vector [], the frequency response is calculated using the default value of 512 samples.

h = freqz(b,a,w) returns the frequency response vector h calculated at the frequencies (in radians per sample) supplied by the vector w. The vector w can have any length.

[h,w] = freqz(b,a,l,'whole') uses n sample points around the entire unit circle to calculate the frequency response. The frequency vector w has length l and has values ranging from 0 to 2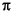 radians per sample.

[h,f] = freqz(b,a,l,fs) returns the frequency response vector h and the corresponding frequency vector f for the digital filter whose transfer function is determined by the (real or complex) numerator and denominator polynomials represented in the vectors b and a, respectively. The vectors h and f are both of length l. For this syntax, the frequency response is calculated using the sampling frequency specified by the scalar fs (in hertz). The frequency vector f is calculated in units of hertz (Hz). The frequency vector f has values ranging from 0 to fs/2Hz.

h = freqz(b,a,f,fs) returns the frequency response vector h calculated at the frequencies (in Hz) supplied in the vector f. The vector f can be any length.

[h,f] = freqz(b,a,l,'whole',fs) uses n points around the entire unit circle to calculate the frequency response. The frequency vector f has length l and has values ranging from 0 to fsHz.

freqz(b,a,...) plots the magnitude and unwrapped phase of the frequency response of the filter. The plot is displayed in the current figure window.

freqz(Hd) plots the magnitude and unwrapped phase of the frequency response of the filter. The plot is displayed in fvtool. The input Hd is a dfilt filter object or an array of dfilt filter objects.

Remarks

It is best to choose a power of 2 for the third input argument n, because freqz uses an FFT algorithm to calculate the frequency response. See the reference description of fft for more information.

Examples

Plot the magnitude and phase response of an FIR filter:

b = fir1(80,0.5,kaiser(81,8));
freqz(b,1);

The same example using a dfilt object and displaying the result in the Filter Visualization Tool (fvtool) is

```
Hd = dfilt.dffir(b);
freqz(Hd);
```

Algorithm

The frequency response [1] of a digital filter can be interpreted as the transfer function evaluated at z = e^j. You can always write a rational transfer function in the following form.

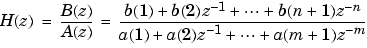
freqz determines the transfer function from the (real or complex) numerator and denominator polynomials you specify, and returns the complex frequency response H(e^j) of a digital filter. The frequency response is evaluated at sample points determined by the syntax that you use.

freqz generally uses an FFT algorithm to compute the frequency response whenever you don't supply a vector of frequencies as an input argument. It computes the frequency response as the ratio of the transformed numerator and denominator coefficients, padded with zeros to the desired length.

When you do supply a vector of frequencies as an input argument, then freqz evaluates the polynomials at each frequency point using Horner's method of nested polynomial evaluation [1], dividing the numerator response by the denominator response.

See Also

abs, angle, fft, filter, freqs, impz, invfreqs, logspace

References

[1] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, pp. 203-205.

freqspace fvtool