

| Signal Processing Toolbox |   |
Discrete Fourier transform using second order Goertzel algorithm
Syntax
Description
goertzel computes the discrete Fourier transform (DFT) of specific indices in a vector or matrix.
y = goertzel(x,i)
returns the DFT of vector x at the indices in vector i, computed using the second-order Goertzel algorithm. If x is a matrix, goertzel computes each column separately. The indices in vector i must be integer values from 1 to N, where N is the length of the first matrix dimension of x that is greater than 1. The resulting y has the same dimensions as x. If i is omitted, it is assumed to be [1:N], which results in a full DFT computation.
y = goertzel(x,i,dim)
returns the discrete Fourier transform (DFT) of matrix x at the indices in vector i, computed along the dimension dim of x.
Note
fft computes all DFT values at all indices, while goertzel computes DFT values at a specified subset of indices (i.e., a portion of the signal's frequency range). If less than log2(N) points are required, goertzel is more efficient than the Fast Fourier Transform (fft).
|
Two examples where goertzel can be useful are spectral analysis of very large signals and dual-tone multifrequency (DTMF) signal detection.
Examples
Generate an 8-Hz sinusoid and use the Goertzel algorithm to detect it using the first 20 indices:
Fs = 1024; Ts = 1/Fs; f = 8; N = 1024; t = Ts*(0:N-1)'; x = sin(2*pi*f*t); % Generate 8 Hz sinusoid figure(1); plot(t,x); figure(2); periodogram(x,[],[],Fs);% Use periodogram to obtain the PSD% (computed with all N points of signal) vec = 1:20; y = goertzel(x,vec);% Now use Goertzel to obtain the PSD figure(3);% only in the region of interest plot(vec-1,20*log10(abs(y)));
Algorithm
goertzel implements this transfer function
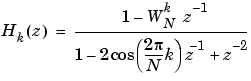
where N is the length of the signal and k is the index of the computed DFT. k is related to the indices in vector i above as k = i - 1.
The signal flow graph for this transfer function is
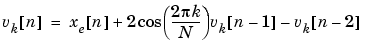
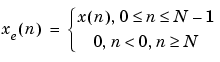
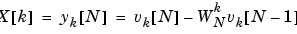
To compute X[k] for a particular k, the Goertzel algorithm requires 4N real multiplications and 4N real additions. Although this is less efficient than computing the DFT by the direct method, Goertzel uses recursion to compute
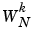 and
and 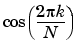
which are evaluated only at n = N. The direct DFT does not use recursion and must compute each complex term separately.
See Also
References
[1] Burrus, C.S. and T.W. Parks. DFT/FFT and Convolution Algorithms. John Wiley & Sons, 1985, pp. 32-26.
[2] Mitra, Sanjit K. Digital Signal Processing: A Computer-Based Approach. New York, NY: McGraw-Hill, 1998, pp. 520-523.
 | gmonopuls | grpdelay |  |
© 1994-2005 The MathWorks, Inc.