grpdelay (Signal Processing Toolbox)

Average filter delay (group delay)

Syntax

grpdelay(b,a)
[gd,w] = grpdelay(b,a,n)
[gd,f] = grpdelay(b,a,n,fs)
[gd,w] = grpdelay(b,a,n,'whole')
[gd,f] = grpdelay(b,a,n,'whole',fs)
gd = grpdelay(b,a,w)
gd = grpdelay(b,a,f,fs)
grpdelay(Hd)

Description

The group delay of a filter is a measure of the average delay of the filter as a function of frequency. It is the negative first derivative of the phase response of the filter. If the complex frequency response of a filter is 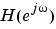, then the group delay is

where 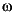is frequency and 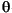theta is the phase angle of .

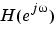grpdelay(b,a) with no output arguments plots the group delay versus frequency in the current figure window.

[gd,w] = grpdelay(b,a,l) returns the i-point group delay, 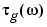, of the digital filter

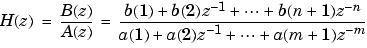
given the numerator and denominator coefficients in vectors b and a. grpdelay returns both gd, the group delay, and w, a vector containing the n frequency points in radians. grpdelay evaluates the group delay at n points equally spaced around the upper half of the unit circle, so w contains n points between 0 and .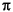

[gd,f] = grpdelay(b,a,n,fs) specifies a positive sampling frequency fs in hertz. It returns a length n vector f containing the actual frequency points at which the group delay is calculated, also in hertz. f contains n points between 0 and fs/2.

[gd,w] = grpdelay(b,a,n,'whole') and

[gd,f] = grpdelay(b,a,n,'whole',fs) use n points around the whole unit circle (from 0 to 2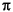, or from 0 to fs).

gd = grpdelay(b,a,w) and

gd = grpdelay(b,a,f,fs) return the group delay evaluated at the points in w (in radians) or f (in hertz), respectively, where fs is the sampling frequency in hertz.

grpdelay(Hd) plots the group delay and displays the plot in fvtool. The input Hd is a dfilt filter object or an array of dfilt filter objects.

grpdelay works for both real and complex filters.

Examples

Plot the group delay of Butterworth filter b(z)/a(z):

[b,a] = butter(6,0.2);
grpdelay(b,a,128)

The same example using a dfilt object and displaying the result in the Filter Visualization Tool (fvtool) is

[b,a] = butter(6,0.2);
Hd=dfilt.df1(b,a);
grpdelay(Hd,128)

Plot both the group and phase delays of a system on the same graph:

gd = grpdelay(b,a,512);
gd(1) = []; % Avoid NaNs
[h,w] = freqz(b,a,512); h(1) = []; w(1) = [];
pd = -unwrap(angle(h))./w;
plot(w,gd,w,pd,':')
xlabel('Frequency (rad/sec)'); grid;
legend('Group Delay','Phase Delay');

Algorithm

grpdelay multiplies the filter coefficients by a unit ramp. After Fourier transformation, this process corresponds to differentiation.

See Also

cceps, fft, freqz, hilbert, icceps, rceps

goertzel hamming