kaiserord (Signal Processing Toolbox)

Kaiser window FIR filter design estimation parameters

Syntax

[n,Wn,beta,ftype] = kaiserord(f,a,dev)
[n,Wn,beta,ftype] = kaiserord(f,a,dev,fs)
c = kaiserord(f,a,dev,fs,'cell')

Description

kaiserord returns a filter order n and beta parameter to specify a Kaiser window for use with the fir1 function. Given a set of specifications in the frequency domain, kaiserord estimates the minimum FIR filter order that will approximately meet the specifications. kaiserord converts the given filter specifications into passband and stopband ripples and converts cutoff frequencies into the form needed for windowed FIR filter design.

[n,Wn,beta,ftype] = kaiserord(f,a,dev) finds the approximate order n, normalized frequency band edges Wn, and weights that meet input specifications f, a, and dev. f is a vector of band edges and a is a vector specifying the desired amplitude on the bands defined by f. The length of f is twice the length of a, minus 2. Together, f and a define a desired piecewise constant response function. dev is a vector the same size as a that specifies the maximum allowable error or deviation between the frequency response of the output filter and its desired amplitude, for each band. The entries in dev specify the passband ripple and the stopband attenuation. You specify each entry in dev as a positive number, representing absolute filter gain (not in decibels).

Note If, in the vector dev, you specify unequal deviations across bands, the minimum specified deviation is used, since the Kaiser window method is constrained to produce filters with minimum deviation in all of the bands.

fir1 can use the resulting order n, frequency vector Wn, multiband magnitude type ftype, and the Kaiser window parameter beta. The ftype string is intended for use with fir1; it is equal to 'high' for a highpass filter and 'stop' for a bandstop filter. For multiband filters, it can be equal to 'dc-0' when the first band is a stopband (starting at f = 0) or 'dc-1' when the first band is a passband.

To design an FIR filter b that approximately meets the specifications given by kaiser parameters f, a, and dev, use the following command.

b = fir1(n,Wn,kaiser(n+1,beta),ftype,'noscale')

[n,Wn,beta,ftype] = kaiserord(f,a,dev,fs) uses a sampling frequency fs in Hz. If you don't specify the argument fs, or if you specify it as the empty vector [], it defaults to 2 Hz, and the Nyquist frequency is 1 Hz. You can use this syntax to specify band edges scaled to a particular application's sampling frequency. The frequency band edges in f must be from 0 to fs/2.

c = kaiserord(f,a,dev,fs,'cell') is a cell-array whose elements are the parameters to fir1.

Note In some cases, kaiserord underestimates or overestimates the order n. If the filter does not meet the specifications, try a higher order such as n+1, n+2, and so on, or a try lower order.

Results are inaccurate if the cutoff frequencies are near 0 or the Nyquist frequency, or if dev is large (greater than 10%).

Remarks

Be careful to distinguish between the meanings of filter length and filter order. The filter length is the number of impulse response samples in the FIR filter. Generally, the impulse response is indexed from n = 0 to n = L-1, where L is the filter length. The filter order is the highest power in a z-transform representation of the filter. For an FIR transfer function, this representation is a polynomial in z, where the highest power is z^L^-1 and the lowest power is z⁰. The filter order is one less than the length (L-1) and is also equal to the number of zeros of the z polynomial.

Examples

Example 1

Design a lowpass filter with passband defined from 0 to 1 kHz and stopband defined from 1500 Hz to 4 kHz. Specify a passband ripple of 5% and a stopband attenuation of 40 dB:

fsamp = 8000;
fcuts = [1000 1500];
mags = [1 0];
devs = [0.05 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
hh = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
freqz(hh)

Example 2

Design an odd-length bandpass filter (note that odd length means even order, so the input to fir1 must be an even integer):

fsamp = 8000;
fcuts = [1000 1300 2210 2410];
mags = [0 1 0];
devs = [0.01 0.05 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
n = n + rem(n,2);
hh = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
[H,f] = freqz(hh,1,1024,fsamp);
plot(f,abs(H)), grid on

Example 3

Design a lowpass filter with a passband cutoff of 1500 Hz, a stopband cutoff of 2000 Hz, passband ripple of 0.01, stopband ripple of 0.1, and a sampling frequency of 8000 Hz:

[n,Wn,beta,ftype] = kaiserord([1500 2000],[1 0],...
                              [0.01 0.1],8000);
b = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');

This is equivalent to

c = kaiserord([1500 2000],[1 0],[0.01 0.1],8000,'cell');
b = fir1(c{:});

Algorithm

kaiserord uses empirically derived formulas for estimating the orders of lowpass filters, as well as differentiators and Hilbert transformers. Estimates for multiband filters (such as bandpass filters) are derived from the lowpass design formulas.

The design formulas that underlie the Kaiser window and its application to FIR filter design are

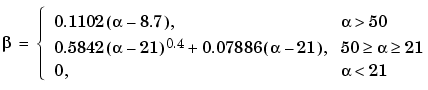
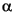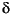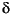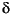where alpha = -20log₁₀ delta is the stopband attenuation expressed in decibels (recall that delta _p = delta _s is required).

The design formula is

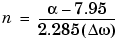
where n is the filter order and 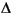capital delta is the width of the smallest transition region.

See Also

fir1, kaiser, firpmord

References

[1] Kaiser, J.F., "Nonrecursive Digital Filter Design Using the - sinh Window Function," Proc. 1974 IEEE Symp. Circuits and Systems, (April 1974), pp. 20-23.

[2] Selected Papers in Digital Signal Processing II, IEEE Press, New York, 1975, pp. 123-126.

[3] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, pp. 458-562.

kaiser lar2rc