fir1 (Signal Processing Toolbox)

Wwindow-based finite impulse response filter design

Syntax

b = fir1(n,Wn)
b = fir1(n,Wn,'ftype')
b = fir1(n,Wn,window)
b = fir1(n,Wn,'ftype',window)
b = fir1(...,'normalization')

Description

fir1 implements the classical method of windowed linear-phase FIR digital filter design [1]. It designs filters in standard lowpass, highpass, bandpass, and bandstop configurations. By default the filter is normalized so that the magnitude response of the filter at the center frequency of the passband is 0 dB.

Note Use fir2 for windowed filters with arbitrary frequency response.

b = fir1(n,Wn) returns row vector b containing the n+1 coefficients of an order n lowpass FIR filter. This is a Hamming-window based, linear-phase filter with normalized cutoff frequency Wn. The output filter coefficients, b, are ordered in descending powers of z.

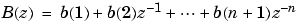
Wn is a number between 0 and 1, where 1 corresponds to the Nyquist frequency.

If Wn is a two-element vector, Wn = [w1 w2], fir1 returns a bandpass filter with passband w1 < 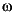< w2.

If Wn is a multi-element vector, Wn = [w1 w2 w3 w4 w5 ... wn], fir1 returns an order n multiband filter with bands 0 < 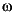< w1, w1 < 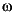< w2, ..., wn < 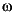< 1.

By default, the filter is scaled so that the center of the first passband has a magnitude of exactly 1 after windowing.

b = fir1(n,Wn,'ftype') specifies a filter type, where 'ftype' is:

'high' for a highpass filter with cutoff frequency Wn.
'stop' for a bandstop filter, if Wn = [w1 w2]. The stopband frequency range is specified by this interval.
'DC-1' to make the first band of a multiband filter a passband.
'DC-0' to make the first band of a multiband filter a stopband.

fir1 always uses an even filter order for the highpass and bandstop configurations. This is because for odd orders, the frequency response at the Nyquist frequency is 0, which is inappropriate for highpass and bandstop filters. If you specify an odd-valued n, fir1 increments it by 1.

b = fir1(n,Wn,window) uses the window specified in column vector window for the design. The vector window must be n+1 elements long. If no window is specified, fir1 uses a Hamming window (see hamming) of length n+1.

b = fir1(n,Wn,'ftype',window) accepts both 'ftype' and window parameters.

b = fir1(...,'normalization') specifies whether or not the filter magnitude is normalized. The string 'normalization' can be the following:

'scale' (default): Normalize the filter so that the magnitude response of the filter at the center frequency of the passband is 0 dB.
'noscale': Do not normalize the filter.

The group delay of the FIR filter designed by fir1 is n/2.

Algorithm

fir1 uses the window method of FIR filter design [1]. If w(n) denotes a window, where 1 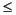n 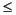N, and the impulse response of the ideal filter is h(n), where h(n) is the inverse Fourier transform of the ideal frequency response, then the windowed digital filter coefficients are given by

Examples

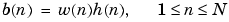
Example 1

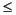
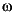
Design a 48th-order FIR bandpass filter with passband 0.35 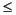0.65:

b = fir1(48,[0.35 0.65]);
freqz(b,1,512)

Example 2

The chirp.mat file contains a signal, y, that has most of its power above fs/4, or half the Nyquist frequency. Design a 34th-order FIR highpass filter to attenuate the components of the signal below fs/4. Use a cutoff frequency of 0.48 and a Chebyshev window with 30 dB of ripple:

load chirp      % Load y and fs.
b = fir1(34,0.48,'high',chebwin(35,30));
freqz(b,1,512)

See Also

cfirpm, filter, fir2, fircls, fircls1, firls, freqz, kaiserord, firpm, window

References

Programs for Digital Signal Processing, IEEE Press, New York, 1979. Algorithm 5.2.

filtstates.dfiir fir2