poly2rc (Signal Processing Toolbox)

Convert prediction filter polynomial to reflection coefficients

Syntax

k = poly2rc(a)
[k,r0] = poly2rc(a,efinal)

Description

k = poly2rc(a) converts the prediction filter polynomial a to the reflection coefficients of the corresponding lattice structure. a can be real or complex, and a(1) cannot be 0. If a(1) is not equal to 1, poly2rc normalizes the prediction filter polynomial by a(1). k is a row vector of size length(a)-1.

[k,r0] = poly2rc(a,efinal) returns the zero-lag autocorrelation, r0, based on the final prediction error, efinal.

A simple, fast way to check if a has all of its roots inside the unit circle is to check if each of the elements of k has magnitude less than 1.

```
stable = all(abs(poly2rc(a))<1)
```

Examples

a = [1.0000   0.6149   0.9899   0.0000   0.0031  -0.0082];
efinal = 0.2;
[k,r0] = poly2rc(a,efinal)
k =
    0.3090
    0.9801
    0.0031
    0.0081
   -0.0082
r0 =
    5.6032

Limitations

If abs(k(i)) == 1 for any i, finding the reflection coefficients is an ill-conditioned problem. poly2rc returns some NaNs and provide a warning message in this case.

Algorithm

poly2rc implements this recursive relationship:

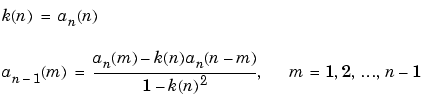
This relationship is based on Levinson's recursion [1]. To implement it, poly2rc loops through a in reverse order after discarding its first element. For each loop iteration i, the function:

Sets k(i) equal to a(i)
Applies the second relationship above to elements 1 through i of the vector a.

```
a = (a-k(i)*fliplr(a))/(1-k(i)^2);
```

See Also

ac2rc, latc2tf, latcfilt, poly2ac, rc2poly, tf2latc

References

[1] Kay, S.M. Modern Spectral Estimation, Englewood Cliffs, NJ, Prentice-Hall, 1988.

poly2lsf polyscale