| Signal Processing Toolbox | |
Generalized Cosine Windows
Blackman, Flat Top, Hamming, Hann, and rectangular windows are all special cases of the generalized cosine window. These windows are combinations of sinusoidal sequences with frequencies 0,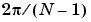 
, and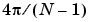 
, where N is the window length. One way to generate them is
where A, B, and C are constants you define. The concept behind these windows is that by summing the individual terms to form the window, the low frequency peaks in the frequency domain combine in such a way as to decrease sidelobe height. This has the side effect of increasing the mainlobe width.
The Hamming and Hann windows are two-term generalized cosine windows, given by A = 0.54, B = 0.46 for Hamming and A = 0.5, B = 0.5 for Hann (C = 0 in both cases). The hamming and hann functions, respectively, compute these windows.
Note that the definition of the generalized cosine window shown in the earlier MATLAB code yields zeros at samples 1 and n for A = 0.5 and B = 0.5.
The Blackman window is a popular three-term window, given by A = 0.42, B = 0.5, C = 0.08. The blackman function computes this window.
The Flat Top window is a five-term window and is used for calibration. It is given by A = 1, B = 1.93, C = 1.29, D =0.388, and E = 0.322.
This WinTool compares Blackman, Hamming, Hann, and Flat Top windows.
The time and frequency domain plots of the length 64 Blackman, Hamming, Hann and Flattop windows are in this illustration. The Hamming window is widest in the time domain, followed by the Hann and Blackman, and finally, Flattop, which is the most narrow. As expected, in the frequency domain, the mainlobe of the Flattop is widest, followed by the narrower Blackman, Hann, and finally Hamming with the most narrow mainlobe.
| | Basic Shapes | Kaiser Window | |
© 1994-2005 The MathWorks, Inc.
